1g of same non volatile solute is added to 100g of two different solvents A and B. Kb of A:B=1:5
Find out (ΔTb)A(ΔTb)B
1:10
1:5
1:20
2:5
The correct Answer is:B
To solve the problem, we need to find the ratio of the boiling point elevation for two different solvents (A and B) when the same non-volatile solute is added to both.
1. Understand the Formula for Boiling Point Elevation:
The boiling point elevation (ΔTb) is given by the formula:
ΔTb=Kb⋅m
where Kb is the ebullioscopic constant of the solvent and m is the molality of the solution.
2. Identify the Given Information:
- Mass of solute = 1 g
- Mass of solvent A = 100 g
- Mass of solvent B = 100 g
- Ratio of Kb for solvents A and B = Kb(A):Kb(B)=1:5
3. Calculate Molality for Solvent A:
Molality (m) is defined as:
m=moles of solutemass of solvent in kg
The moles of solute can be calculated as:
moles=1 gM=1M
where M is the molar mass of the solute (in grams per mole). The mass of solvent A in kg is:
100 g=0.1 kg
Therefore, the molality of A is:
mA=1/M0.1=10M
4. Calculate Molality for Solvent B:
The mass of solvent B is also 100 g, which is:
0.1 kg
Thus, the molality of B is the same as A since the mass of solute and solvent are the same:
mB=1/M0.1=10M
5. Calculate the Ratio of Boiling Point Elevation:
Now we can express the boiling point elevation for both solvents:
ΔTbA=Kb(A)⋅mA=Kb(A)⋅10M
ΔTbB=Kb(B)⋅mB=Kb(B)⋅10M
Taking the ratio of the boiling point elevations:
ΔTbAΔTbB=Kb(A)⋅mAKb(B)⋅mB=Kb(A)Kb(B)⋅mAmB
6. Substituting the Known Values:
Since Kb(A):Kb(B)=1:5, we have:
Kb(A)Kb(B)=15
And since mA=mB, we have:
mAmB=1
Therefore:
ΔTbAΔTbB=15⋅1=15
Final Answer:
ΔTbAΔTbB=15
The boiling point elevation (ΔTb) is given by the formula:
ΔTb=Kb⋅m
where Kb is the ebullioscopic constant of the solvent and m is the molality of the solution.
- Mass of solute = 1 g
- Mass of solvent A = 100 g
- Mass of solvent B = 100 g
- Ratio of Kb for solvents A and B = Kb(A):Kb(B)=1:5
Molality (m) is defined as:
m=moles of solutemass of solvent in kg
The moles of solute can be calculated as:
moles=1 gM=1M
where M is the molar mass of the solute (in grams per mole). The mass of solvent A in kg is:
100 g=0.1 kg
Therefore, the molality of A is:
mA=1/M0.1=10M
The mass of solvent B is also 100 g, which is:
0.1 kg
Thus, the molality of B is the same as A since the mass of solute and solvent are the same:
mB=1/M0.1=10M
Now we can express the boiling point elevation for both solvents:
ΔTbA=Kb(A)⋅mA=Kb(A)⋅10M
ΔTbB=Kb(B)⋅mB=Kb(B)⋅10M
Taking the ratio of the boiling point elevations:
ΔTbAΔTbB=Kb(A)⋅mAKb(B)⋅mB=Kb(A)Kb(B)⋅mAmB
Since Kb(A):Kb(B)=1:5, we have:
Kb(A)Kb(B)=15
And since mA=mB, we have:
mAmB=1
Therefore:
ΔTbAΔTbB=15⋅1=15
ΔTbAΔTbB=15
Topper's Solved these Questions
Similar Questions
2g of a non - volatile, non-electrolyte solute is dissolved in 100 g of two different solvents X and Y whose
Kb values are in the ratio of 1 : 4 The value of (ΔTb(X)ΔTb(Y)) is _________View SolutionTwo solutions of non-volatile and non-electrolyte solute A and B are prepared separately. The molar mass ratio MAMB=13. Both are prepared as 5% by weight solution in water. Then what is the ratio of freezing point depresions, (ΔTf)A(ΔTf)B of the solutions?
View Solution
Knowledge Check
- Question 1 - Select One
1g of a non-volatile non-electrolyte solute is dissolved in 100g of two different solvents A and B whose ebullioscopic constants are in the ratio of 1 : 5. The ratio of the elevation in their boiling points, ΔTb(A)ΔTb(B) is
A1:0.2B1:5C5:1D10:1 - Question 2 - Select One
1g of a non-volatile non-electrolyte solute is dissolved in 100g of two different solvents A and B whose ebullioscopic constants are in the ratio of 1 : 5. The ratio of the elevation in their boiling points, ΔTb(A)ΔTb(B) is
A5:1B10:1C1:5D1:3 - Question 3 - Select One
20 g of a non-volatile solute is added to 500 g of solvent. Freezing point of solvent =5.48∘C and solution =4.47∘C.Kf=1.93∘/m. Molecular mas of the solute is
A72.2B76.4C73.2D70.6
Two solutions of non-volatile solutes A and B are prepared. The molar mass ratio, MAMB=13. Both are prepared as 5% solutions by weight in water. Calculate the ratio of the freezing point depressions. (ΔTf)A(ΔTf)B of the solutions. If the two solutions are mixed to prepared two new solutions S1 and S2, the mixing ratio being 2:3 and 3:2 by volume for S1 and S2 respectively what would be the ratio (ΔTf)S1(ΔTf)S2?
View Solutionwhen 1.80g of a nonvolatile solute is dissolved in 90g of benzene, the boiling point is raised to 354.11K. If the boiling point of benzene is 353.23K and Kb for benzene is 2.53KKgmol−1, calculate the molecular mass of the solute.
Strategy: From the boiling point of the solution, calculate the boiling point elevation, ΔTb, then solve the equation ΔTb=Kbm for the molality m. Molality equals moles of solute divided by kilograms of solvent (benzene). By substituting values for molality and kilograms C6H6, we can solve for moles of solute. The molar mass of solute equals mass of solute (1.80g) divided by moles of solute. The molecular mass (in amu) has the same numerical value as molar mass in gmol−1.View SolutionConsider following figure and answer the questions at the end of it. Figure explains elevation in boiling point when a non-volatile solute is added to a solvent.
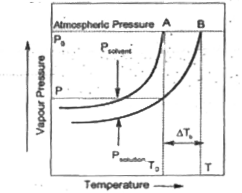
Variation of vapour pressure with temperature and showing elevation in boiling point.
Given that ΔTb is the elevation in boiling point of the solvent in a solution of molality m then Ltm→0(ΔTbm) is equal toView SolutionConsider following figure and answer the questions at the end of it.
Figure explains elevation in boiling point when a non-volatile solute is added to a solvent.
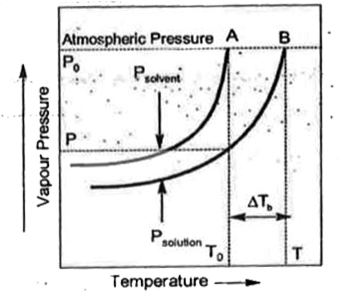
Variation of vapour pressure with temperature and showing elevation in boiling point.
Given that ΔTb is the elevation in boiling point of the solvent in a solution of molality 'm' then Ltm→0(DηlTbm) is equal toView SolutionFigure explains elevation in boiling point when a non-volatile solute is added to a solvent. Variation of vapour pressure with temperaure and elevation in boiling point is marked.

Ratio of ΔTb/Kb of 6%AB2 and 9%A2B(AB2 and A2B both are non-electrolytes) is 1 mol/kg in both cases. Hence, atomic masses of A and B are respectively.View Solution

