Three portion A , B and C each of mass re placed ina line with AB=BC=d. Find the gravittional force on a fourth article P of same mass placed at a distance d from the particle B on the perpendicular bisector of the line AC.
 The force ast P due to A is
The force ast P due to A is
FA=Gm2(AP)2=Gm22d2
along PA. the force at P due to C is
FC=Gm2(CP)2=Gm22d2
along PC. The force at P due to B is
FB=Gm2d2 along PB
The resultant of FA,FBandFc will be along PB. Clearly ∠APB=∠BPC=45∘
Component of FA and PB=FAcos5∘=Gm22√2d2
component of FC along PB=FCcos45∘=Gm22√2d2
component of FBalongPB=Gm2d2
Hence the resultant of three forces is
Gm2d2)12√2+12√2)+1)=Gm2d2(1+1√2) along PB.
Topper's Solved these Questions
- GRAVITATIONBOOK - HC VERMACHAPTER - GRAVITATIONEXERCISE - Short Answer
19 Videos
- GRAVITATIONBOOK - HC VERMACHAPTER - GRAVITATIONEXERCISE - Objective 1
17 Videos
- GRAVITATIONBOOK - HC VERMACHAPTER - GRAVITATIONEXERCISE - Exercises
39 Videos
- FRICTIONBOOK - HC VERMACHAPTER - FRICTIONEXERCISE - Exercises
31 Videos
- HEAT AND TEMPERATUREBOOK - HC VERMACHAPTER - HEAT AND TEMPERATUREEXERCISE - Exercise
4 Videos
Similar Questions
A tunnel is dug along a diameter of the earth. Find the force on a particle of mass m placed in the tunnel at a distance x from the centre.
View SolutionThree identical particles each of mass m are placed at the vertices of an equilateral triangle of side a. Fing the force exerted by this system on a particle P of mass m placed at the

(a) the mid point of a side
(b) centre of the triangle
View Solution
Knowledge Check
Two particles each of mass 'm' are placed at A and C are such AB=BC=L. The gravitational force on the third particle placed at D at a distance L on the perpendicular bisector of the line AC is
AGm2L2 along BDBGm2√2L2 along DBCGm2L2 along ACDGm2√2L2 along BDThree equal masses each of mass 'm' are palced at the three corners of an equilateral of side a
If a fourth particle of equal mass is placed at the centre of triangle then net force acting on it is equal to .AGm2a2B4Gm23a2C3Gm2a2DzeroThree equal masses each of mass 'm' are palced at the three corners of an equilateral of side a
If a fourth particle of equal mass is placed at the centre of triangle then net force acting on it is equal to .AGm2a2B4Gm23a2C3Gm2a2Dzero
Three equal masses m are placed at the three corners of an equilateral tringle of side a. find the force exerted by this sytem on another particle of mass m placed at a. the mid point of a side b. at the centre of the triangle.
View SolutionA thin shell of mass m and radius R is fixed. Two particles of same mass m are fixed at point A and B on the shell such that AB subtends an angle of 120∘ at the centre. A particle of mass m is held at point C inside the shell which is on perpendicular bisector of line AB. Find the velocity of mass at C when it reaches the opposite end of the point C on the shell under the influence of gravitational field.
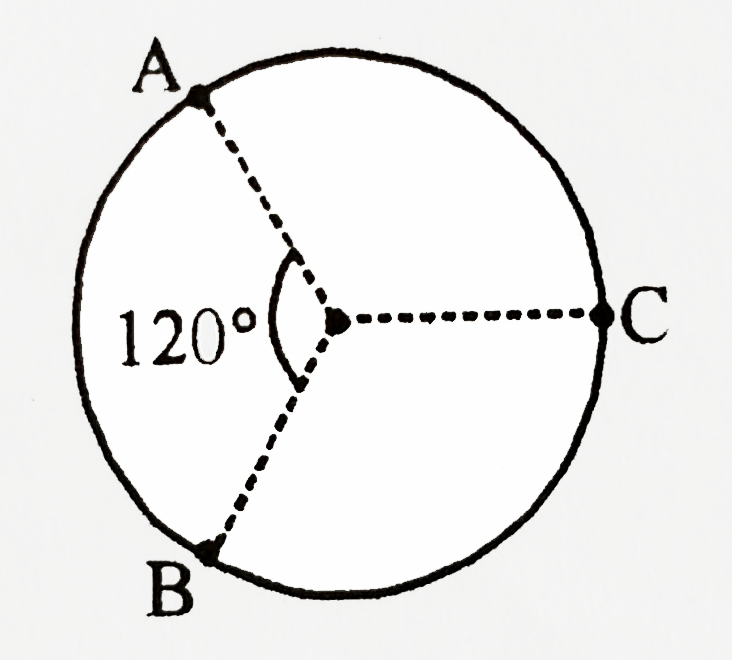
View SolutionTwo particles A and B having equal charges are placed at distance d apart. A third charged particle placed on the perpendicular bisector at a distance x will experience the maximum Coulomb’s force when :
View SolutionTwo point masses, each equal to M, are placed a distance 2a apart. Show that a small mass m placed midway between them on the line joining them will be in equilibrium and if it is slightly displaced from this position along the line perpendicular to the line joining the masses, it will execute simple harmonic oscillations. Calculate the frequnency of these oscillations.
View SolutionWe know that when two equal masses are placed on a line then, gravitational force on a third mass is zero due to these two masses when the third is placed at the centre of line joining the two masses. But if third mass is placed anywhere else on the x-axis, the gravitational force acts on that mass due to these two masses. Consider a system shown in figure.
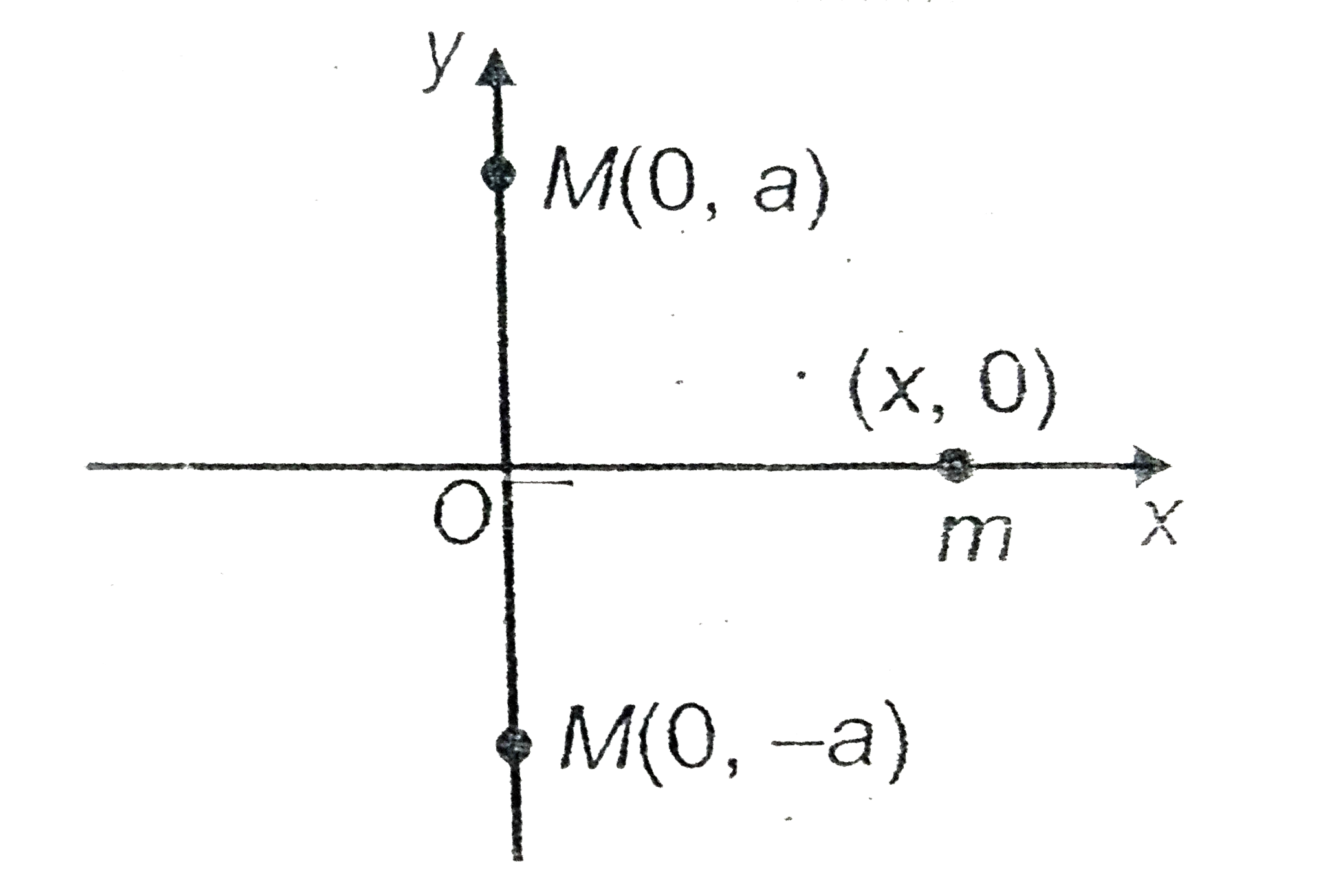
In this system two point masses of mass M each are placed at y-axis at a distance a from origin and these masses are fixed. If a third point mass of mass m is released at a distance x from origin on x-axis, then answer the following questions.
The distance between positions of maximum force on mass m is
View Solution
