A uniform disc of radius 5.0 cm and mass 200g is fixed at its centre to a metal wire, the other end of which is fixed with a clamp. The hanging disc is rotated about the wire through an angle and is released. If the disc makes torsional oscillations with time period 0.20s, find the torsional constant of the wire.
The situation is shown in ure. The moment of inertia of the disc about the wire is
I=mr22=(0.20kg)(5.0×10−2m)22
=2.5×106−4kg−m2 The time period is given by
T=2π√lk
or k=4π2IT2
=4π2(2.5×10−4kg−m2)(0.20s)2
=0.25kg−m2s2
 .
.
Topper's Solved these Questions
- SIMPLE HARMONIC MOTIONBOOK - HC VERMACHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Worked Out Examples
22 Videos
- SIMPLE HARMONIC MOTIONBOOK - HC VERMACHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Short Answer
13 Videos
- ROTATIONAL MECHANICSBOOK - HC VERMACHAPTER - ROTATIONAL MECHANICSEXERCISE - Exercises
86 Videos
- SOME MECHANICAL PROPERTIES OF MATTERBOOK - HC VERMACHAPTER - SOME MECHANICAL PROPERTIES OF MATTEREXERCISE - Exercises
32 Videos
Similar Questions
A uniform of radius 5.0cm and mass 200g is fixed at its centre to a metal wire , the other end of which is fixed to a celling. The hanging disc is rotate about the wire through an angle and is released. If the disc makes torsional oscillations with time period 0.20s , find the torsional constant of the wire.

View SolutionA uniform disc of mass m and radius r is suspended through a wire attached to its centre. If the time period of the torsional oscillations be T, what is the torsional constant of the wire?
View Solution
Knowledge Check
A circular disc fixed at its centre to a metal wire and the other end of the wire is clamped. The disc is rotated about the wire as axis and is released. The disc about this axis makes simple harmonic oscillations with a frequency of 12Hz. If moment of inertia of the disc about this axis is 0.1 kg −m2, the torsional constant of the wire is
A0.99 kg m2s−2B0.45 kg m2s−2C09.9 kg m2s−2D0.49 kg m2s−2A metal rod of length 'L' and mass 'm' is piovted at one end. A thin disk of mass 'M' and radius 'R'(<L). Is attached at its centre to the free end of the rod. Consider two ways the disc is attached: (case A). The disc is not free to rotate about its centre and (case B) the disc is free to rotate about its center. The rod-disc sustem perform SHM in vertical plane after being released from the same displaced potion. Which of the following statement(s) is (are) true?
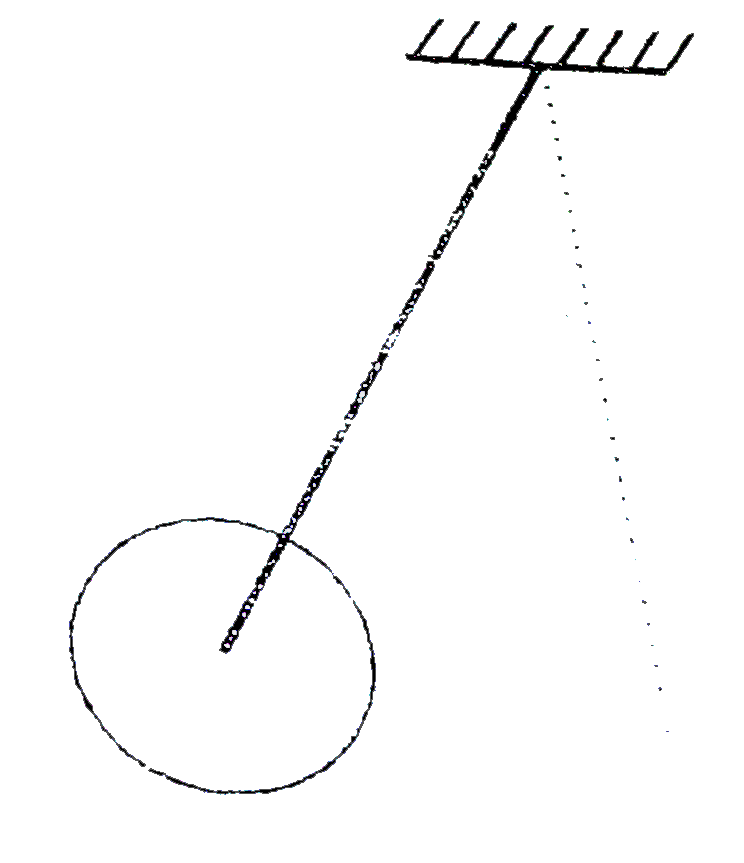 ARestoring torque in case A = Restoring torque in caseBBRestoring torque in case A< Restoring torque in caseBCRestoring frequency case A> Angular frequency for caseBDRestoring frequency case A< Angular frequency for caseB
ARestoring torque in case A = Restoring torque in caseBBRestoring torque in case A< Restoring torque in caseBCRestoring frequency case A> Angular frequency for caseBDRestoring frequency case A< Angular frequency for caseBA uniform circular disc of mass 200 g and radius 5 cm is rotated about one of its dimeters at an angular speed of 15 rad/sec. What is the angular momentum about the axis of ratation ?
A16×10−2JsB18.75×10−4JsC19×10−4JsD22×10−2Js
A circular disc of mass 12 kg is suspended by a wire attached to its centre. The wire is twisted by rotating the disc and then released, so that the time period of torsional oscillation is 2 s. If the radius of the disc is 10 cm, then calculate the torsional spring constant of the wire.
View SolutionA circular disc of mass 10kg is suspended by a wire attahced to its centre. The wire is twisted by rotating the disc and released. The period of torsional oscillations is found to be 1.5s. The radius of the disc is 15cm. Determing the torsional spring constant of the wire. (Torsional spring constant α is definied by the relation J=−αθ, where J is the restoring coubple and θ the angle of twist.
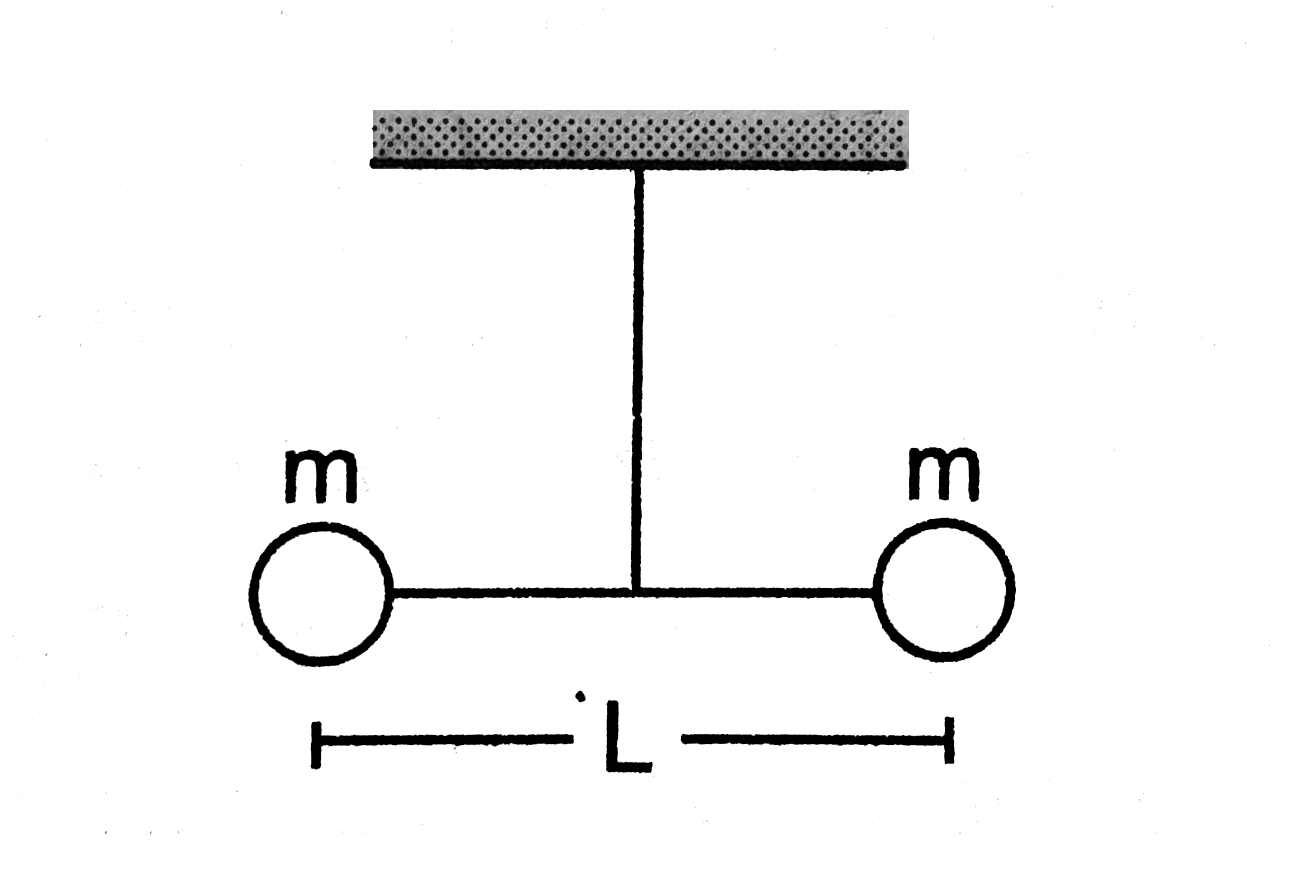
View SolutionTwo small balls, each of mass m are connected by a light rigid rod of length L. The system is suspended from its centre by a thin wire of torsional constant k. The rod is rotated about the wire through an angle θ0 and released. Find the tension in the rod as the system passes through the mean position.
View Solution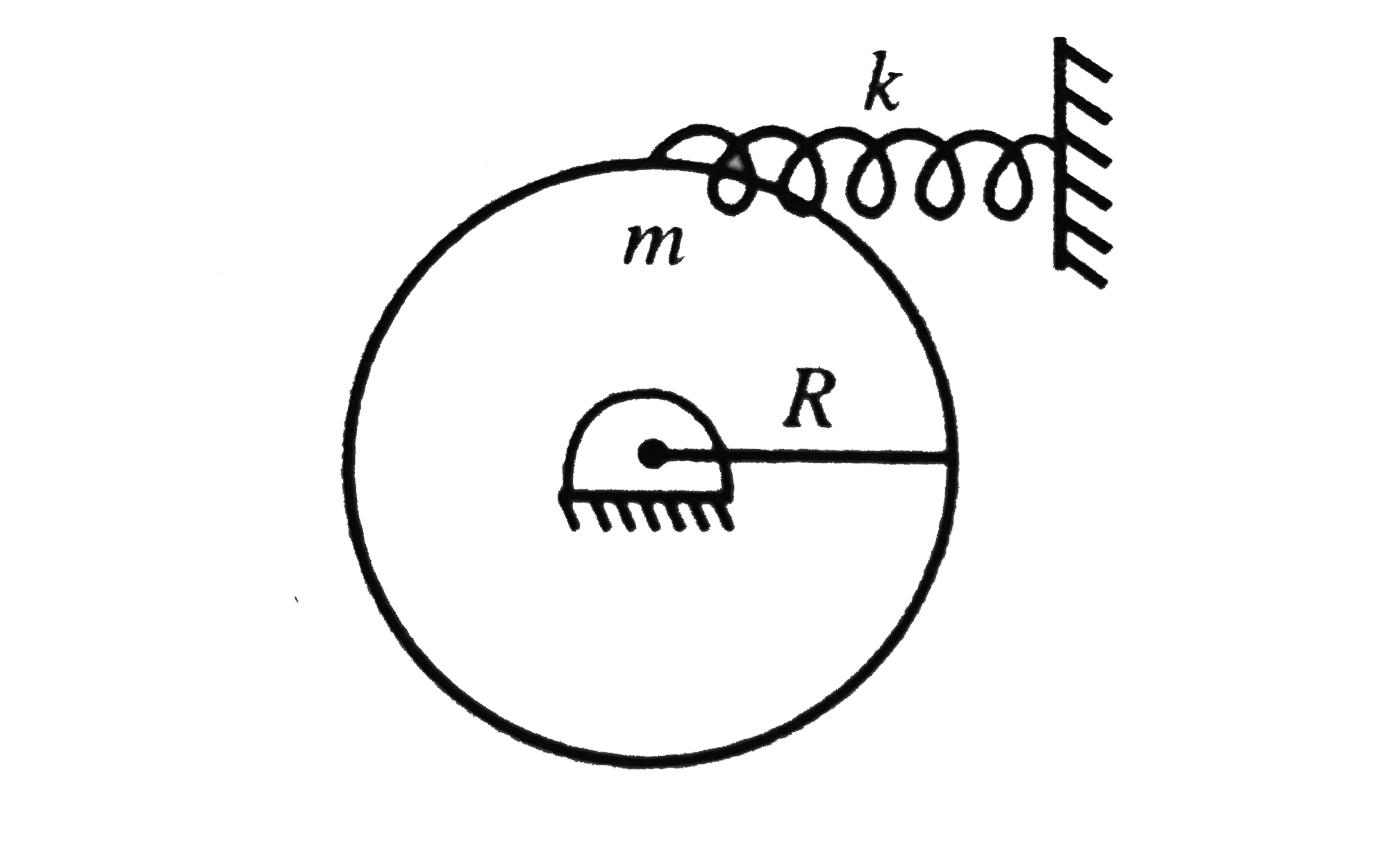
A uniform disc of mass m and radius R is pivoted smoothly at its centre of mass. A light spring of stiffness k is attached with the dics tangentially as shown in the Fig. Find the angular frequency in rads of torsional oscillation of the disc. (Take m=5kg and K=10Nm.)
View SolutionA unifrom circular disc of mass 200g and radius 4cm is rotated about one of its diameters at an angular speed of 10rad/s. Find its abgular momentum about the axis of rotation ?
View Solution
