The force acting on a particel moving along X-axis is F=−(x−v0t)wherek is a positive constant An observer moving at a constant velocity v0 along the X-axis looks the prticle . What kind of motion does he find for the particle?
Step by step video & image solution for The force acting on a particel moving along X-axis is F=-(x-v_0t) where k is a positive constant An observer moving at a constant velocity v_0 along the X-axis looks the prticle . What kind of motion does he find for the particle? by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- SIMPLE HARMONIC MOTIONBOOK - HC VERMACHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Objective 1
21 Videos
- SIMPLE HARMONIC MOTIONBOOK - HC VERMACHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Objective 2
14 Videos
- SIMPLE HARMONIC MOTIONBOOK - HC VERMACHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Worked Out Examples
22 Videos
- ROTATIONAL MECHANICSBOOK - HC VERMACHAPTER - ROTATIONAL MECHANICSEXERCISE - Exercises
86 Videos
- SOME MECHANICAL PROPERTIES OF MATTERBOOK - HC VERMACHAPTER - SOME MECHANICAL PROPERTIES OF MATTEREXERCISE - Exercises
32 Videos
Similar Questions
STATEMENT -1 :The force acting on a particle moving alongx -axis is F=−α(x+vt), where α is a constant.
and
STATEMENT-2 : To anobserver moving along x-axis with constant velocity v, it represents SHM.
View SolutionForce acting on a particle moving along x-axis as shown in figure. Find points of stable and unstable equlibrium.
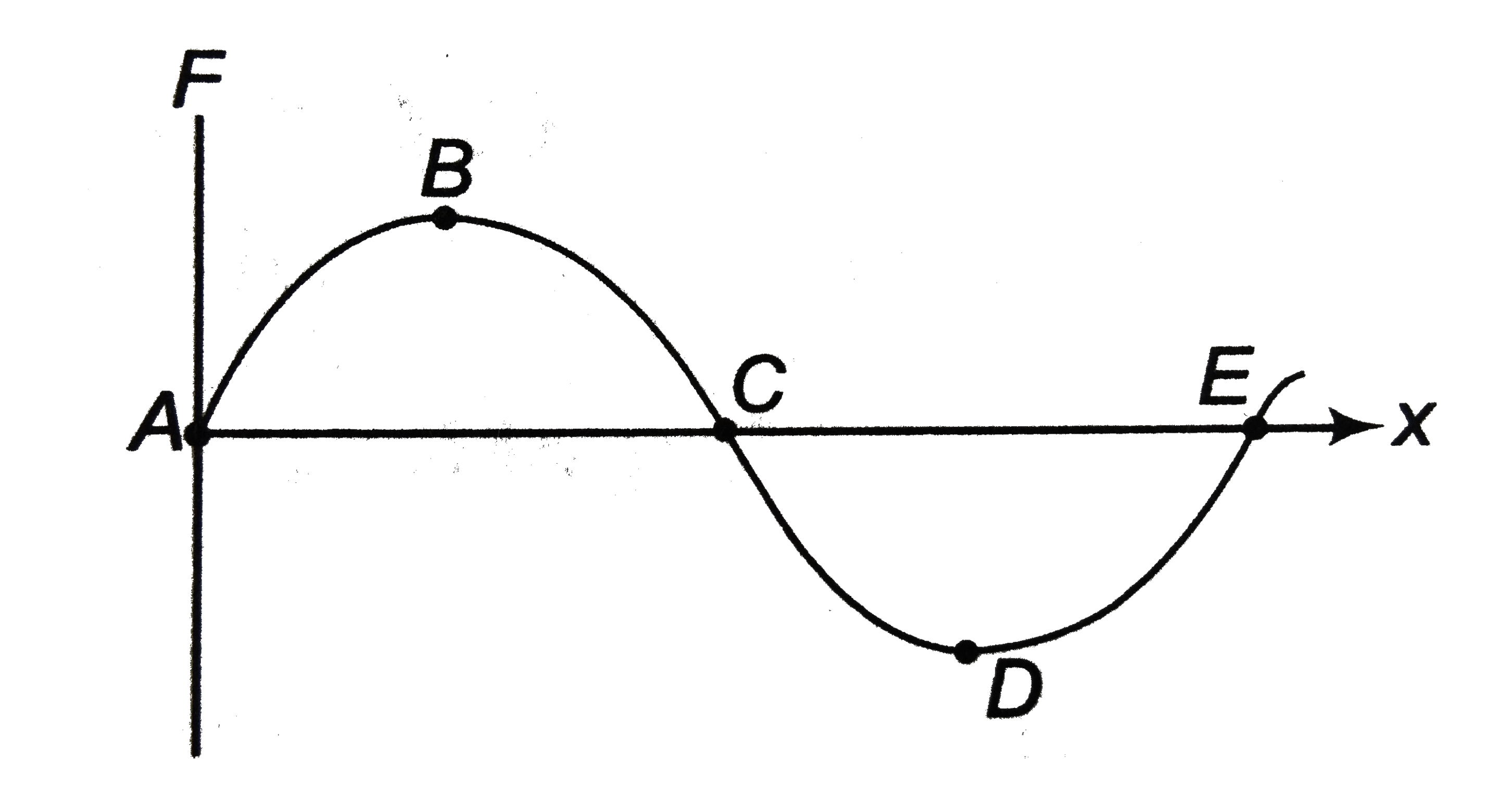 .
.
View Solution
Knowledge Check
A force F=−kx3 is acting on a block moving along x-axis. Here, k is a positive constant. Work done by this force is
Apositive in displacing the block from x = 3 to x = 1Bpositive in displacing the block from x = - 1 to x = - 3Cnegative in displacing the block from x = 3 to x = 1Dnegative in displacing the block from x = - 1 to x = - 3The force acting on a body moving along x-axis varies with the position of the particle shown in the figure. The body is in stable equilibrium at
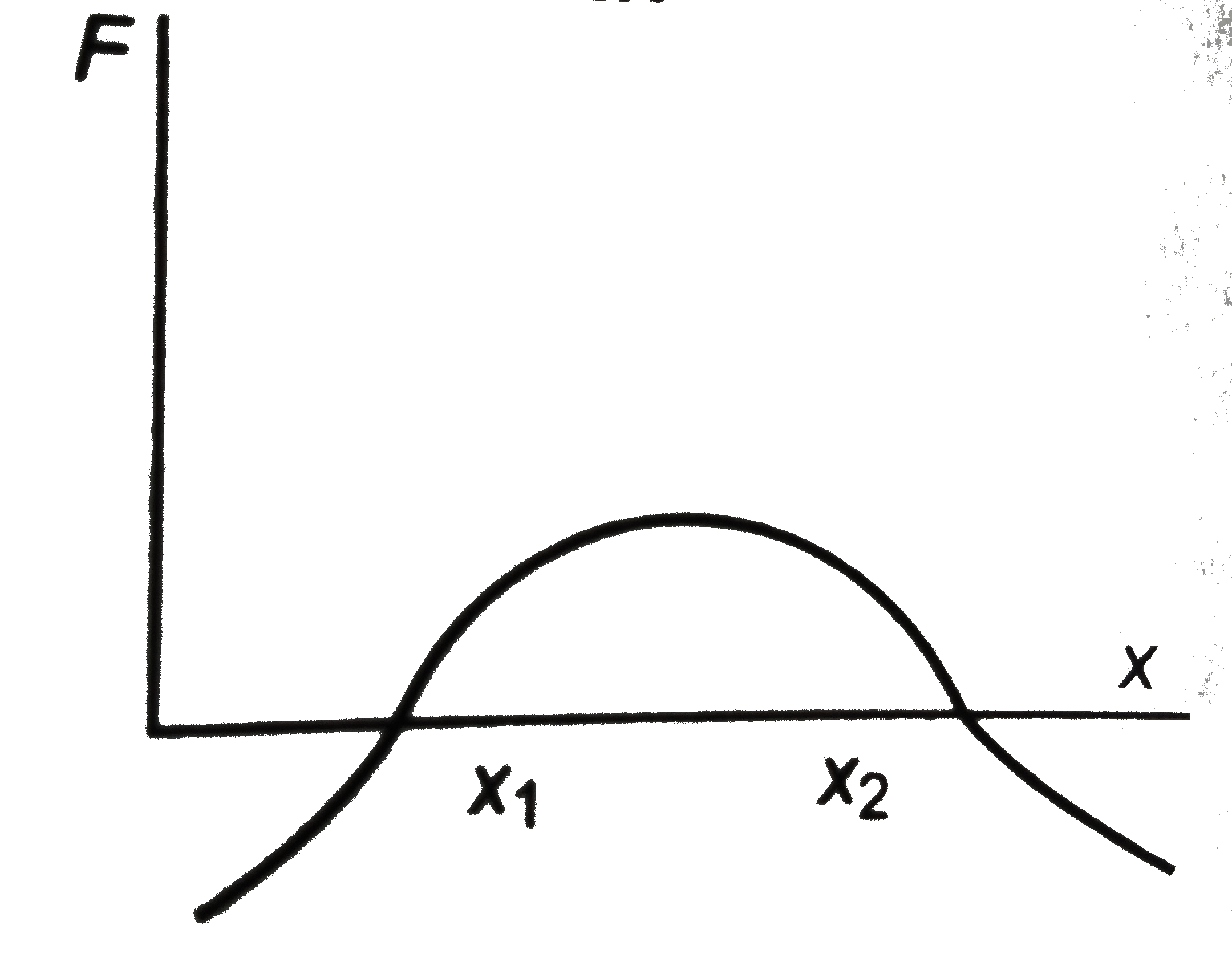 . Ax=x1Bx=x2Cboth x1 and x2Dneither x1 nor x2
. Ax=x1Bx=x2Cboth x1 and x2Dneither x1 nor x2The position x of particle moving along x-axis varies with time t as x=Asin(ωt) where A and ω are positive constants. The acceleration a of particle varies with its position (x) as
Aa=AxBa=−ω2xCa=AωxDa=ω2xA
The velocity of a particle moving in the positive direction of the X-axis varies as V=K√S where K is a positive constant. Draw V−t graph.
View SolutionThe magnitude of force acting on a particle moving along x-axis varies with time (t) as shown in figure. If at t = 0 the velocity of particle is v0, then its velocity at t=T0 will be

View SolutionA particle moves along x-axis with acceleration a=6(t−1) where t is in second. If the particle is initially at the origin and it moves along positive x-axis with v0=2m/s, find the nature of motion of the particle.
View SolutionThe velocity of a particle moving along the xaxis is given by v=v0+λx, where v0 and lambda are constant. Find the velocity in terms of t.
View SolutionIf v is the velocity of a body moving along x-axis, then acceleration of body is
View Solution
