A barometer kept in an elevator accelerating upward reads 76 cm. The air pressure in the elevator is
76cm
lt76cm
gt76cm
zero
The correct Answer is:C
To find the air pressure in an elevator that is accelerating upward and where a barometer reads 76 cm of mercury, we can follow these steps:
Step 1: Understand the basic principle of a barometer
A barometer measures atmospheric pressure by balancing the weight of a column of mercury against the atmospheric pressure. The height of the mercury column (H) is related to the pressure (P) by the equation:
P=H⋅ρ⋅g
where:
- P is the atmospheric pressure,
- H is the height of the mercury column,
- ρ is the density of mercury,
- g is the acceleration due to gravity.
Step 2: Consider the effect of the elevator's acceleration
When the elevator accelerates upward with an acceleration a, the effective gravitational acceleration becomes:
g′=g+a
This means that the pressure exerted by the mercury column in the barometer will also change because the effective weight of the mercury column increases.
Step 3: Write the modified pressure equation
In the accelerating elevator, the pressure at the bottom of the mercury column can be expressed as:
P′=H⋅ρ⋅(g+a)
where P′ is the pressure in the elevator.
Step 4: Relate the pressures
Since the barometer reads 76 cm of mercury, we can substitute H=76cm into the equation:
P′=76cm⋅ρ⋅(g+a)
Step 5: Compare the pressures
The pressure at sea level (normal atmospheric pressure) is given by:
P=76cm⋅ρ⋅g
Since g+a>g, it follows that:
P′=76cm⋅ρ⋅(g+a)>76cm⋅ρ⋅g=P
Conclusion
Thus, the air pressure in the elevator is greater than the normal atmospheric pressure of 76 cm of mercury.
Final Answer
The air pressure in the elevator is greater than 76 cm of mercury.
---
A barometer measures atmospheric pressure by balancing the weight of a column of mercury against the atmospheric pressure. The height of the mercury column (H) is related to the pressure (P) by the equation:
P=H⋅ρ⋅g
where:
- P is the atmospheric pressure,
- H is the height of the mercury column,
- ρ is the density of mercury,
- g is the acceleration due to gravity.
When the elevator accelerates upward with an acceleration a, the effective gravitational acceleration becomes:
g′=g+a
This means that the pressure exerted by the mercury column in the barometer will also change because the effective weight of the mercury column increases.
In the accelerating elevator, the pressure at the bottom of the mercury column can be expressed as:
P′=H⋅ρ⋅(g+a)
where P′ is the pressure in the elevator.
Since the barometer reads 76 cm of mercury, we can substitute H=76cm into the equation:
P′=76cm⋅ρ⋅(g+a)
The pressure at sea level (normal atmospheric pressure) is given by:
P=76cm⋅ρ⋅g
Since g+a>g, it follows that:
P′=76cm⋅ρ⋅(g+a)>76cm⋅ρ⋅g=P
Thus, the air pressure in the elevator is greater than the normal atmospheric pressure of 76 cm of mercury.
The air pressure in the elevator is greater than 76 cm of mercury.
Topper's Solved these Questions
- FLUID MECHANICSBOOK - HC VERMACHAPTER - FLUID MECHANICSEXERCISE - Objective 2
8 Videos
- FLUID MECHANICSBOOK - HC VERMACHAPTER - FLUID MECHANICSEXERCISE - Exercises
35 Videos
- FLUID MECHANICSBOOK - HC VERMACHAPTER - FLUID MECHANICSEXERCISE - Short Answer
16 Videos
- CIRCULAR MOTIONBOOK - HC VERMACHAPTER - CIRCULAR MOTIONEXERCISE - Exercises
30 Videos
- FRICTIONBOOK - HC VERMACHAPTER - FRICTIONEXERCISE - Exercises
31 Videos
Similar Questions
A barometer kept in an alevator ac celerating upward reads 76 cm of mrecury. If the elevator is ac celerating upwards at 4.5ms−2 find the air pressure in the elevator in cm of mercury. Density of mercuty =13.6×103kgm−3G=9.8m/s2
View SolutionA barometer kept in an elevator accelerating upwards reads 76 cm of Hg. If the elevator is accelerating upwards at 4.9ms−2 , what will be the air pressure in the elevator?
View Solution
Knowledge Check
A barometer kept in a stationary elevator reads 76cm. If the element starts accelerating up the reading will be
AZeroBEqual to 76cmCMore than 76cmDLess than 76cmA block of mass m is suspended by a light thread from an elevator. The elevator is accelerating upward with uniform acceleration a. The work done by tension on the block during t seconds is (u = 0)
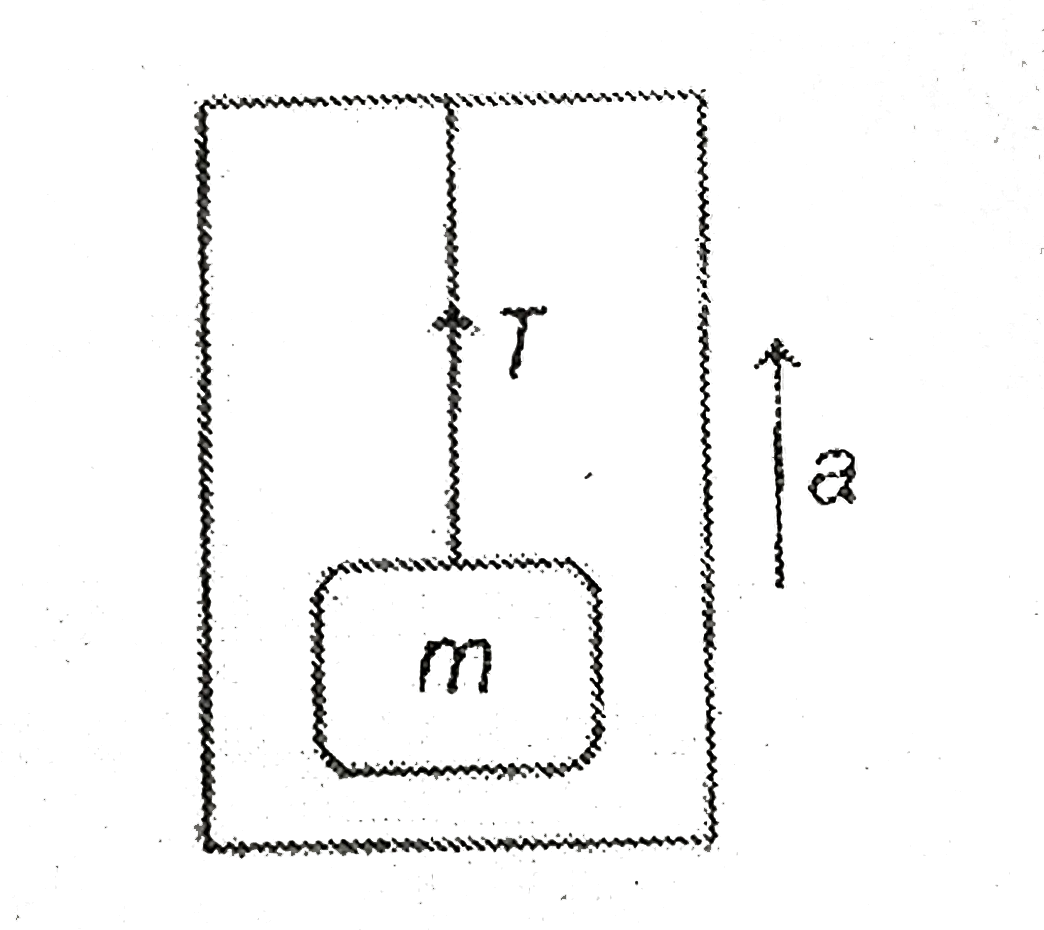 Am2(g+a)at2Bm2(g−a)at2Cm2gat2D0
Am2(g+a)at2Bm2(g−a)at2Cm2gat2D0A barometer kept in a lift reads 11 cm of mercury, when the lift is stationary. Then the lift starts moving down with an acceleration a, where a lt g. What is the air pressure in the lift, as read by the barometer ?
AρghBρ(g+a)Cρ(g−a)Dρgha
A barometer is kept in an elevator accelerating upwards at 4.9m/s2. If the barometer reads 77 cm of Hg, what will be the air pressure in the elevator?
View SolutionAn elevator is accelerating downwards with an acceleration of 4.9 ms−2. A barometer placed in this elevator reads 75 cm of Hg. Calculate the air pressure inside the elevator.
View SolutionA barometer kept in an elevator reads 76 cm when it is at rest. If the elevator goes up with increasing speed, the reading will be
View SolutionA barometer accelerating downwards reads 76 cm of Hg. What will be the possible air pressure inside the jar?
View SolutionA 5- kg body is suspendel from a spring - balance , and an identical body is balanced on a pan of a physical balance . If both the balances are kept in an elevator , then what would happen in each case when the elevator is moving with an upward acceleration ?
View Solution
