A hollow spherical body of inner and outer radii 6 cm, and 8 cm respectively floats half submerged in water. Find the density of the material of the sphere.
The correct Answer is:C
To find the density of the material of a hollow spherical body that is half submerged in water, we can follow these steps:
Step 1: Understand the Problem
We have a hollow sphere with inner radius r1=6 cm and outer radius r2=8 cm. The sphere is floating half submerged in water. We need to find the density of the material of the sphere.
Step 2: Calculate the Volume of the Hollow Sphere
The volume V of the hollow sphere can be calculated using the formula for the volume of a sphere:
V=43π(r32−r31)
Substituting the values of r1 and r2:
V=43π(83−63)
Calculating 83 and 63:
83=512and63=216
Thus,
V=43π(512−216)=43π(296)
Step 3: Calculate the Weight of the Sphere
The weight of the sphere W is given by:
W=mg
where m is the mass of the sphere. The mass can be expressed in terms of density ρ and volume V:
m=ρV
Thus,
W=ρVg
Step 4: Calculate the Buoyant Force
The buoyant force Fb acting on the half-submerged sphere is equal to the weight of the water displaced by the submerged part of the sphere. Since the sphere is half submerged, the volume of water displaced is:
Vb=V2
The buoyant force can be expressed as:
Fb=ρwaterVbg
where ρwater is the density of water (approximately 1g/cm3). Thus,
Fb=ρwater(V2)g
Step 5: Set Up the Equation
Since the sphere is floating, the weight of the sphere is equal to the buoyant force:
ρVg=ρwater(V2)g
We can cancel g from both sides:
ρV=ρwater(V2)
Step 6: Simplify the Equation
Cancelling V from both sides (assuming V≠0):
ρ=ρwater2
Step 7: Substitute the Values
Substituting ρwater=1g/cm3:
ρ=12=0.5g/cm3
Step 8: Final Calculation
Now we need to calculate the density of the material of the sphere using the volume we calculated earlier:
ρ=mV
Substituting m=ρV:
ρ=ρVV=ρ
Conclusion
The density of the material of the sphere is:
ρ≈0.864g/cm3
We have a hollow sphere with inner radius r1=6 cm and outer radius r2=8 cm. The sphere is floating half submerged in water. We need to find the density of the material of the sphere.
The volume V of the hollow sphere can be calculated using the formula for the volume of a sphere:
V=43π(r32−r31)
Substituting the values of r1 and r2:
V=43π(83−63)
Calculating 83 and 63:
83=512and63=216
Thus,
V=43π(512−216)=43π(296)
The weight of the sphere W is given by:
W=mg
where m is the mass of the sphere. The mass can be expressed in terms of density ρ and volume V:
m=ρV
Thus,
W=ρVg
The buoyant force Fb acting on the half-submerged sphere is equal to the weight of the water displaced by the submerged part of the sphere. Since the sphere is half submerged, the volume of water displaced is:
Vb=V2
The buoyant force can be expressed as:
Fb=ρwaterVbg
where ρwater is the density of water (approximately 1g/cm3). Thus,
Fb=ρwater(V2)g
Since the sphere is floating, the weight of the sphere is equal to the buoyant force:
ρVg=ρwater(V2)g
We can cancel g from both sides:
ρV=ρwater(V2)
Cancelling V from both sides (assuming V≠0):
ρ=ρwater2
Substituting ρwater=1g/cm3:
ρ=12=0.5g/cm3
Now we need to calculate the density of the material of the sphere using the volume we calculated earlier:
ρ=mV
Substituting m=ρV:
ρ=ρVV=ρ
The density of the material of the sphere is:
ρ≈0.864g/cm3
Topper's Solved these Questions
Similar Questions
A small filament is at the centre of a hollow glass sphere of inner and outer radii 8 cm and 9 cm respectively. The refractive index of glass is 1.50. Calculate the position of the image of the filament when viewed from outside the sphere.
View SolutionA hollow sphere of internal and external radii 2 cm and 4 cm respectively is melted into a cone of base radius 4 cm. Find the height and slant height of the cone.
View Solution
Knowledge Check
In a conducting hollow sphere of inner and outer radii 5 cm and 10 cm, respectively, a point charge 1 C is placed at point A, that is 3 cm from the center C of the hollow sphere. An external uniform electric field to magnitude 20NC−1 is also applied. Net electric force on this charge is 15 N, away from the center of the sphere as shown. Find the magnitude of net force exerted on the charge placed at point A by the induced charges on the sphere
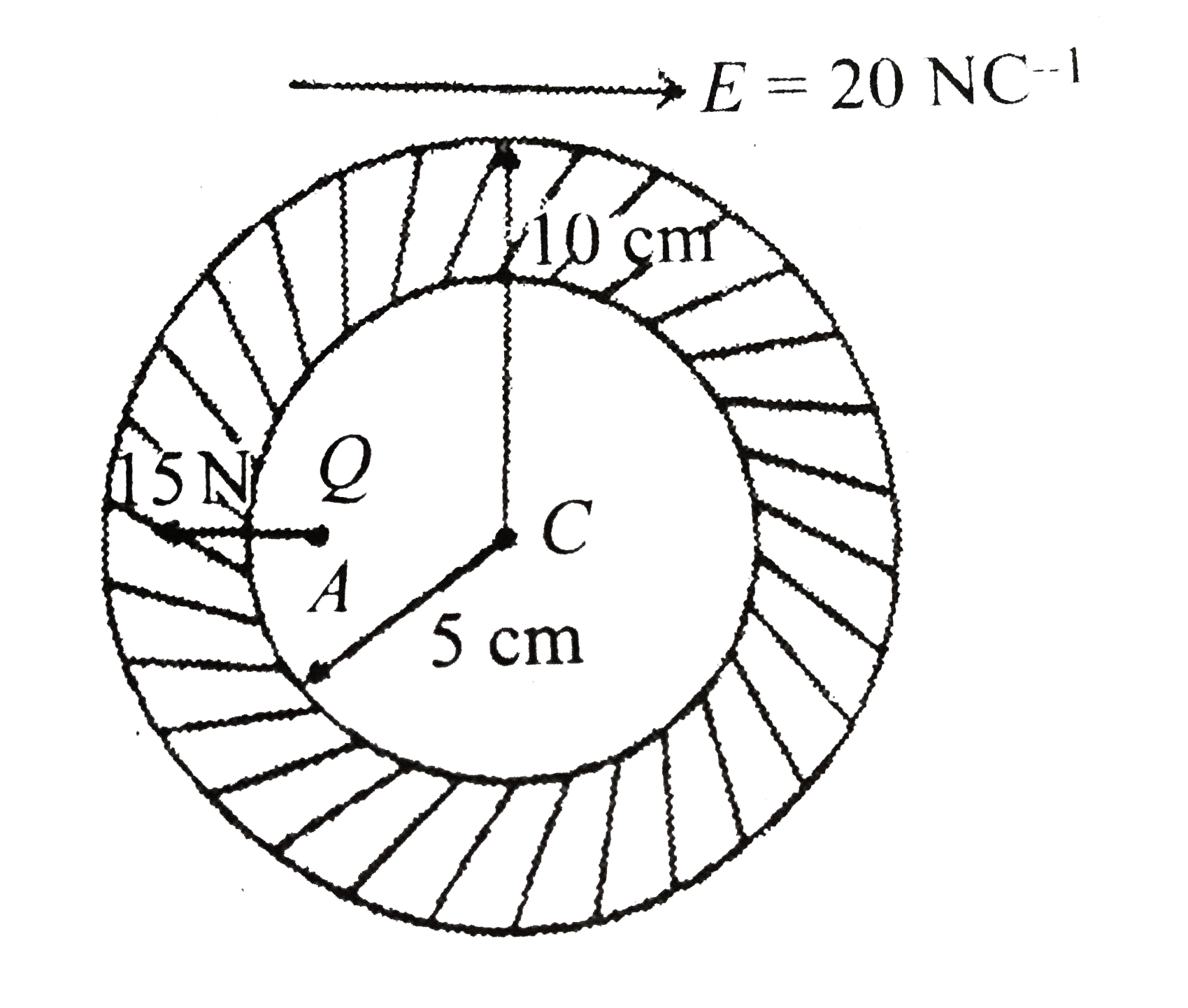 A15 NB20 NC5 ND35 N
A15 NB20 NC5 ND35 NA hollow sphere of internal and external diameters 4 cm and 8 cm respectively is melted into a cone of base diameter 8 cm. Calculate the height of the cone.
A16 cmB14 cmC32 cmDNone of theseA hollow sphere of internal and external diameters 6 cm and 10 cm respectively is melted into a right circular cone of diameter 8 cm. The height of the cone is
A22.5 cmB23.5 cmC24.5 cmD25.5 cm
A hollow sphere of inner radius 8.0 cm and outer radius 9.0 cm floats half-submerged in a liquid of density 820 kg/m3. (a) What is the mass of the sphere? (b) Calculate the density of the material of which the sphere is made.
View SolutionA hollow sphere of innder radius 9 cm and outer radius 10 cm floats half-submerged in a liquid of specific gravity 0.8. calculate the density of the material of which the sphere is made. What would be the density of a liquid in which the hollow sphere would just floats completely sumberged. ?
View SolutionA hollow metallic sphere has inner and outer radii, respectively as 5 cm and 10 cm if the mass of the sphere is 2.5 kg, find (a) density of the material, (b) relative density of the material of the sphere.
View SolutionA hollow sphere of internal and external diameters 4cm and 8cm respectively is melted into a cone of base diameter 8cm. What is the height of the cone
View SolutionA hollow sphere of internal and external diameters 4 cm and 8 cm respectively is melted into a cone of base diameter 8 cm. Calculate the height of the cone.
View Solution
