A cubical metal block of edge 12 cm floats in mercry with one fifth of the height inside the mercury. Water poured till the surface of the block is just immersed in it. Find the height of the block is just immersed in it. Find the height of the water column to be poured. Specific gravity of mercury =13.6.
The correct Answer is:A, C, D
To solve the problem, let's break it down step by step.
Step 1: Understand the problem
We have a cubical metal block with an edge length of 12 cm floating in mercury. The block is floating such that one-fifth of its height is submerged in mercury. We need to find the height of the water column that needs to be poured until the block is completely immersed.
Step 2: Calculate the submerged height of the block in mercury
The total height of the block is 12 cm. Since one-fifth of the height is submerged in mercury:
Submerged height in mercury=15×12 cm=2.4 cm
Step 3: Calculate the volume of the block
The volume V of the cubical block can be calculated using the formula for the volume of a cube:
V=edge3=123=1728 cm3
Step 4: Calculate the weight of the block
The weight of the block W can be expressed in terms of its density ρb and volume V:
W=ρb⋅V⋅g
where g is the acceleration due to gravity. However, since we are looking for a ratio, we can ignore g for now.
Step 5: Calculate the buoyant force acting on the block
The buoyant force Fb acting on the block is equal to the weight of the mercury displaced by the submerged part of the block:
Fb=ρHg⋅VHg⋅g
Where VHg is the volume of mercury displaced. The volume of mercury displaced is equal to the submerged volume of the block:
VHg=Submerged height×Base area=2.4 cm×(12 cm)2=2.4×144=345.6 cm3
Step 6: Calculate the density of mercury
Given that the specific gravity of mercury is 13.6, the density of mercury ρHg can be calculated as:
ρHg=13.6×ρwater=13.6×1 g/cm3=13.6 g/cm3
Step 7: Set up the equilibrium condition
At equilibrium, the weight of the block is equal to the buoyant force:
ρb⋅V=ρHg⋅VHg
Substituting the values we have:
ρb⋅1728=13.6⋅345.6
Step 8: Solve for the density of the block
Calculating the right side:
13.6⋅345.6=4693.76
Now we can find ρb:
ρb=4693.761728≈2.72 g/cm3
Step 9: Calculate the height of the water column
When water is poured, the total volume of the block will be equal to the volume of mercury plus the volume of water:
V=VHg+Vwater
Let x be the height of the water column. The volume of water is:
Vwater=x⋅(122)=144x
The volume of mercury will be:
VHg=(12−x)⋅(122)=144(12−x)
Setting up the equation:
1728=345.6+144x
Solving for x:
1728−345.6=144x1382.4=144xx=1382.4144≈9.6 cm
Final Answer
The height of the water column to be poured is approximately 9.6 cm.
We have a cubical metal block with an edge length of 12 cm floating in mercury. The block is floating such that one-fifth of its height is submerged in mercury. We need to find the height of the water column that needs to be poured until the block is completely immersed.
The total height of the block is 12 cm. Since one-fifth of the height is submerged in mercury:
Submerged height in mercury=15×12 cm=2.4 cm
The volume V of the cubical block can be calculated using the formula for the volume of a cube:
V=edge3=123=1728 cm3
The weight of the block W can be expressed in terms of its density ρb and volume V:
W=ρb⋅V⋅g
where g is the acceleration due to gravity. However, since we are looking for a ratio, we can ignore g for now.
The buoyant force Fb acting on the block is equal to the weight of the mercury displaced by the submerged part of the block:
Fb=ρHg⋅VHg⋅g
Where VHg is the volume of mercury displaced. The volume of mercury displaced is equal to the submerged volume of the block:
VHg=Submerged height×Base area=2.4 cm×(12 cm)2=2.4×144=345.6 cm3
Given that the specific gravity of mercury is 13.6, the density of mercury ρHg can be calculated as:
ρHg=13.6×ρwater=13.6×1 g/cm3=13.6 g/cm3
At equilibrium, the weight of the block is equal to the buoyant force:
ρb⋅V=ρHg⋅VHg
Substituting the values we have:
ρb⋅1728=13.6⋅345.6
Calculating the right side:
13.6⋅345.6=4693.76
Now we can find ρb:
ρb=4693.761728≈2.72 g/cm3
When water is poured, the total volume of the block will be equal to the volume of mercury plus the volume of water:
V=VHg+Vwater
Let x be the height of the water column. The volume of water is:
Vwater=x⋅(122)=144x
The volume of mercury will be:
VHg=(12−x)⋅(122)=144(12−x)
Setting up the equation:
1728=345.6+144x
Solving for x:
1728−345.6=144x1382.4=144xx=1382.4144≈9.6 cm
The height of the water column to be poured is approximately 9.6 cm.
Topper's Solved these Questions
Similar Questions
A cubical block of iron 5 cm on each side is floating on mercury in a vessel. (i) what is the height of the block above mercury level ?
(ii) Water is poured in the vessel unitl it just covers the iron block. What is the height of water column . density of mercur 13.6gm/cm3. Density of iron 7.2 gm/cm3
View SolutionOne third height of a cubical block of edge 6cm is floating in kerosene oil of specific gravity 0.8. To make the block to be just immersed some water is poured. What is the height of the water column?
View Solution
Knowledge Check
A matallic block weighs 15N in air. It weights 12N when immersed in water and 13N when immersed in another liquid. What is the specific gravity of the liquid?
A1/3B2/3C12/13D13/15A cubical block of copper of side 10cm is floating in a vessel containing mercury. Water is poured into the vessel so that the copper block just gets submerged. The height of water column is
(ρHg=13.6g/cc,ρCu=7.3g/cc,ρwater=1gm/cc)A1.25 cmB2.5cmC5cmD7.5cm
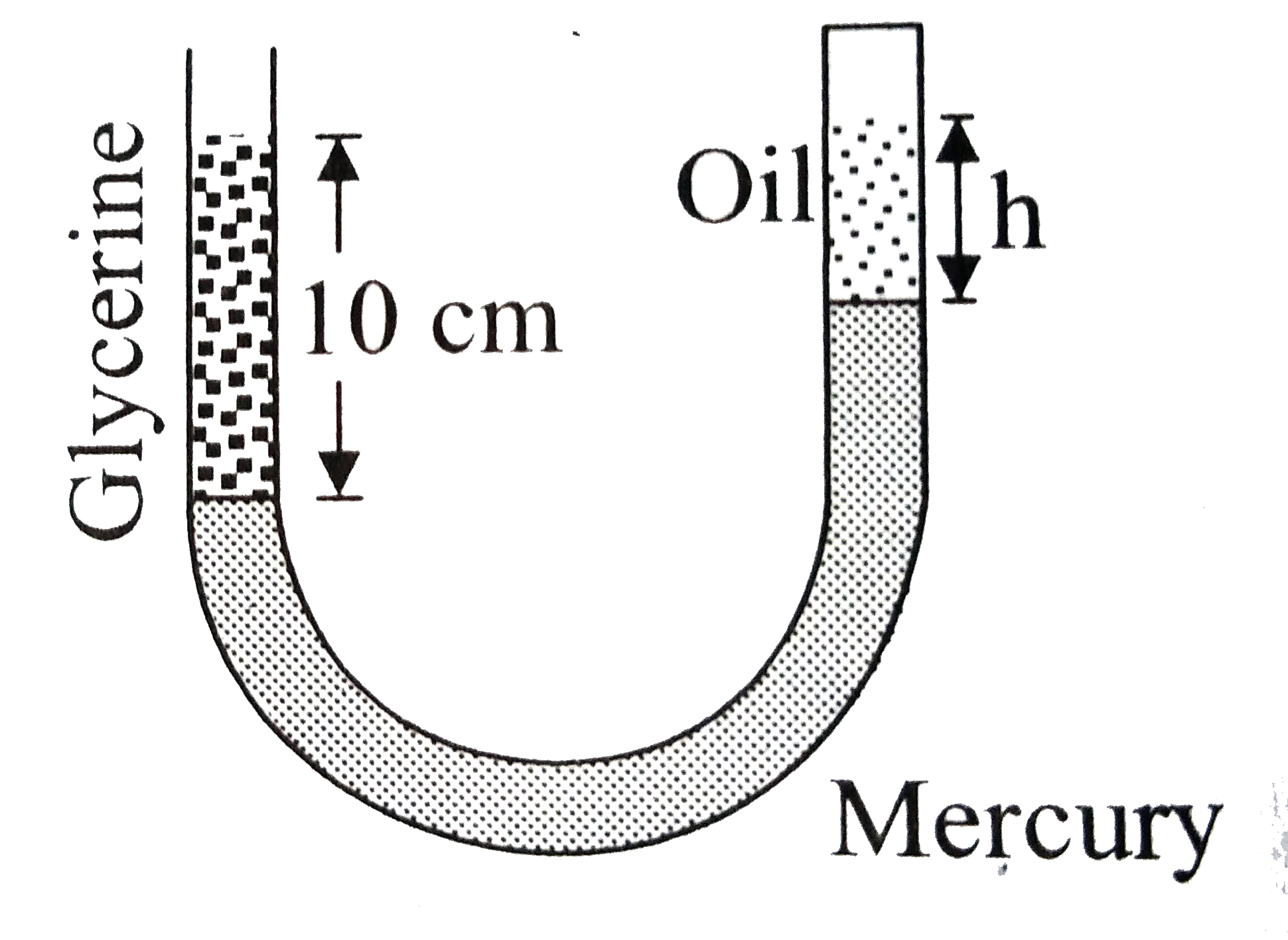
A vertical U-tube of uniform inner cross section contains mercury in both sides of its arms. A glycerin (density =1.3g/cm3) column of length 10 cm is introduced into one of its arms. Oil of density 0.8 gm/cm3 is poured into the other arm until the upper surfaces of the oil and glycerin are in the same horizontal level. Find the length of the same horizontal level. Find the length of the oil column, Density of mercury =13.6g/cm3
View SolutionA cube of iron of edge 5cm floats on the surface of mercury, contained in a tank. Water is then poured on top, so that the cube just gets immersed. Find the depth of water layer. (Specific gravities of iron-and mercury are 7.8 and 13.6, respectively.)
View SolutionA cubical block of ice floating in water has to suport metal piece weighing 0.5 kg. What can be the minimum edge of the block so that it does not sink in water/ specific gravity of ice=0.9.
View SolutionA cubical block of water is dipped completely in water. Each edge of the block is 1 cm is length. Find the bouyant force acting on the block.
View SolutionThe liquids shown in figure in the two arms are mercury (specific gravity =13.6) and water. If the difference of heights of the mercury columns is 2 cm, find the height of the water column.
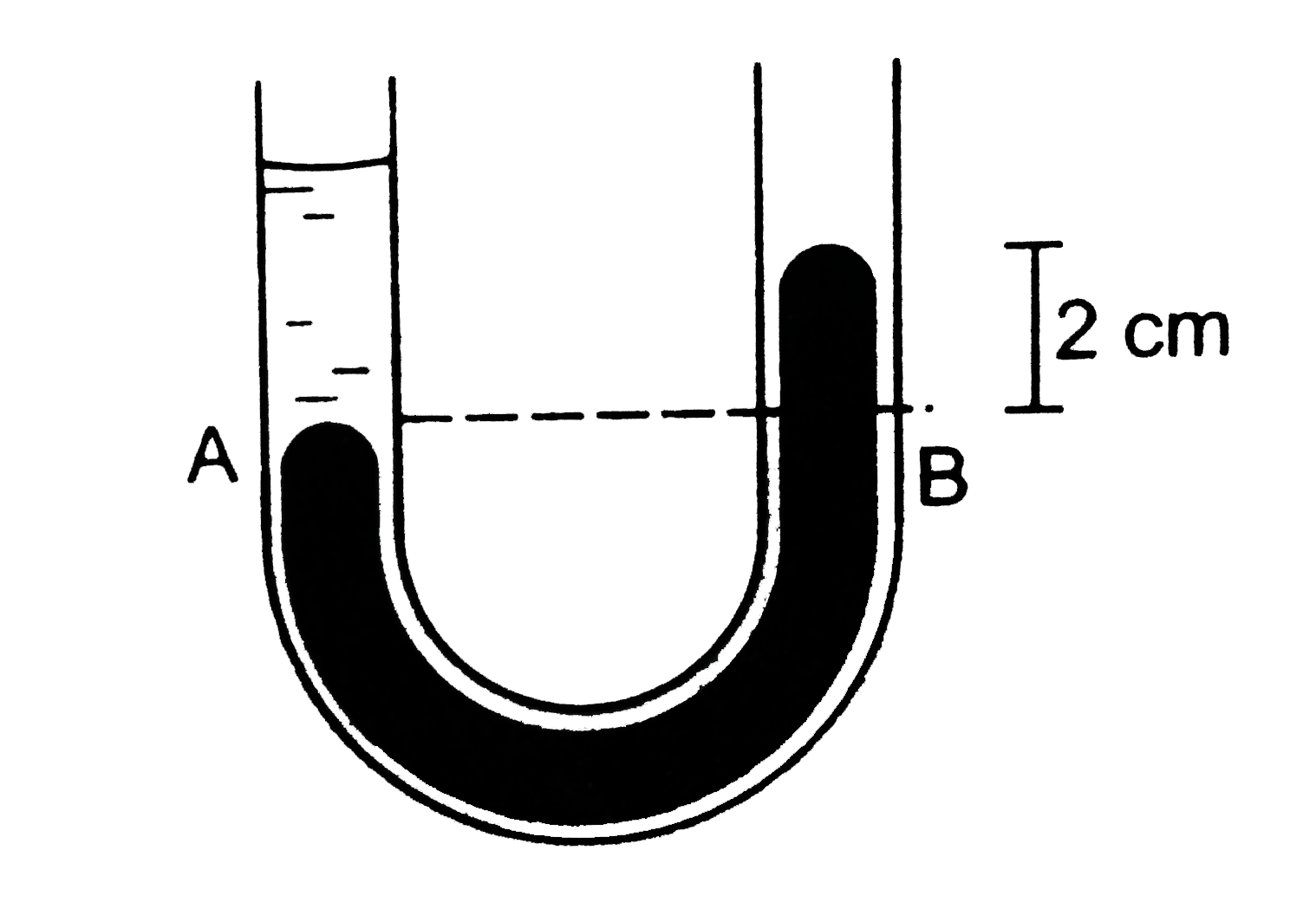 ,
,
View SolutionA cone of a radius 5 cm is filled with water. If the water poured in a cylinder of radius 10cm, the height of the water rises 2 cm, find the height of the cone.
View Solution