A pulse travelling on a string is represented by the function
y=a^3/((x-vt)^2+a^2)
where a=5 mm and v=20 cms^-1. Sketch the shape of the string at t=0, 1 s and 2s. Take x=0 in the middle of the string.
The correct Answer is:A
The pulse is given by
y=⎡⎢
⎢⎣(a)3[(x−vt)2+a2)⎞⎟
⎟⎠⎤⎥
⎥⎦
a=5mm
=0.5cm
v=20cms At t=0s,y=a3(x2+a2)
The graph between y and x can be plotted by talking different vaues of x.
(left as excercse for the studen). ltbr>gt similarly at t=1 s,
y=a3{(x−v)2+a2]
and at t=2s, y=a^3/({(x-2v)^2+a^2})
Topper's Solved these Questions
Similar Questions
Knowledge Check
A transverse wave travelling on a stretched string is is represented by the equation
y=2(2x−6.2t)2+20. Then ,Avelocity of the wave is 3.1m/sBamplitude of the wave is 0.1mCfrequency of the wave is 20HzDwavelength of the wave is 1m
Figure shows a wave pulse at t=0. The pulse moves to the right with a speed of 10cms^-1. Sketch the shape of the string at t=s, 2s and 3s.

View SolutionA wave pulse on a horizontal string is represented by the function
y(x,t)=5.01.0+(x−2t)2 (CGS units)
plot this function at t=0,2.5 and 5.0s.
View SolutionA wave pulse on a horizontal string is represented by the function
y(x,t)=5.01.0+(x−2t)2 (CGS units)
plot this function at t=0,2.5 and 5.0s.
View SolutionFollowing figure shows two wave pulses at t = 0 travelling on a string in opposite directions with the same wave speed 50 cm s1. Sketch the shape of the string at t = 4 ms, 6 ms, 8 ms, and 12 ms.
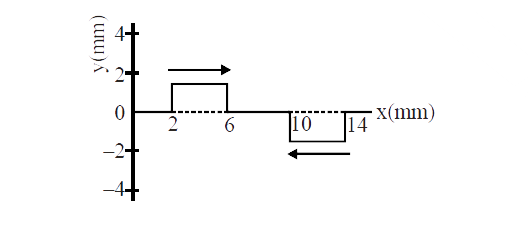
View SolutionA wave pulse is travelling on a string at 2 m/s. displacement y of the particle at x = 0 at any time t is given by
y=2t2+1
Find
(ii) Shape of the pulse at t = 0 and t = 1s.
View SolutionTwo pulses travelling in opposite directions along a string are shown for t=0 in the figure. Plot the shape of the string at t= 1.0, 2.0, 3.0, 4.0 and 5.0s respectively .

View SolutionTwo pulses travelling in opposite directions along a string are shown for t=0 in the figure. Plot the shape of the string at t= 1.0, 2.0, 3.0, 4.0 and 5.0s respectively .

View Solution
