If A={(x,y):y=e−x} and B={(x,y):y=−x}. Then,
A∩B=ϕ
A⊂B
B⊂A
A∩B={(0,1),(0,0)}
The correct Answer is:A
Given that, A={(x,y):y=e−x}
and B={(x,y):y=−x}
Now, drawing both curves
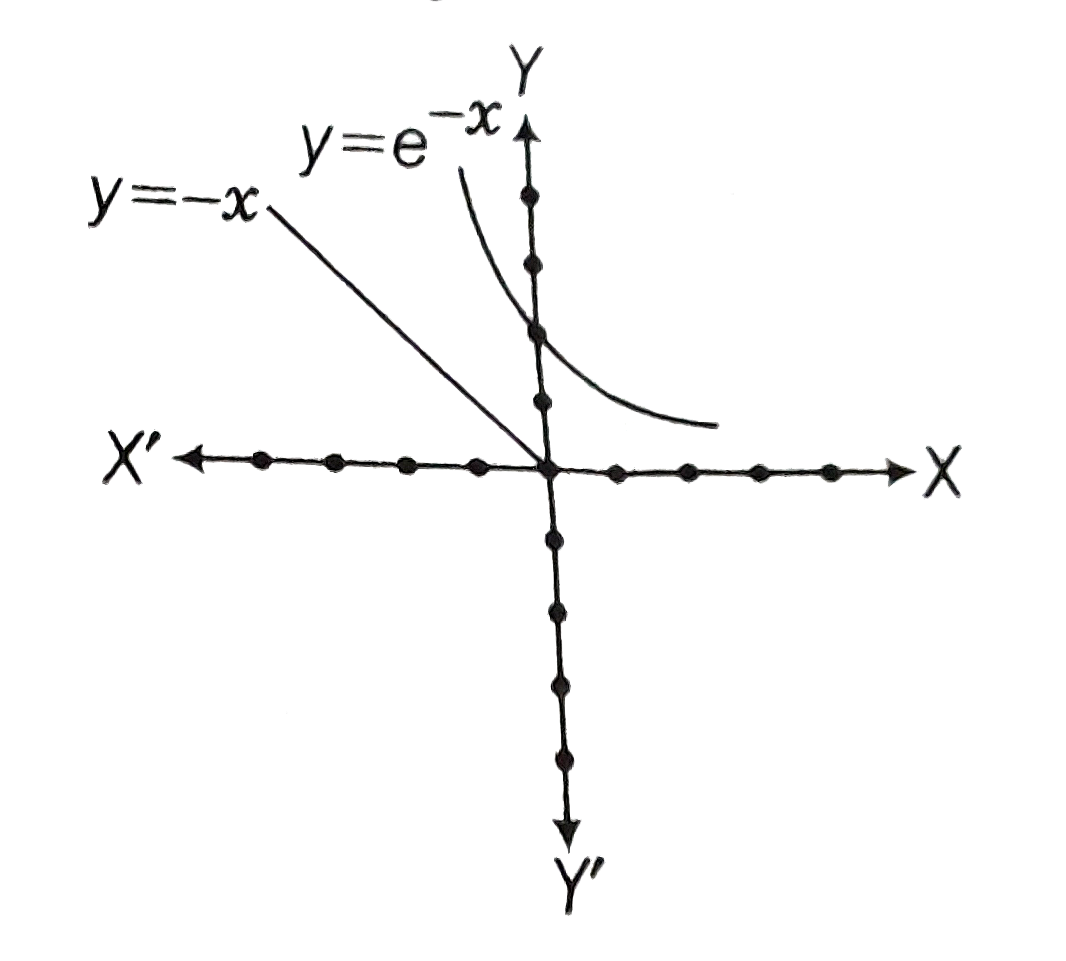
since, both graphs do not intersect each other at any point.
∴A∩B=ϕ [disjoint]
Topper's Solved these Questions
Similar Questions
Knowledge Check
if set A and B are defined as A={(x,y):y=ex,x∈R}
B={(x,y):y=x,x∈R}.thenAB⊂ABA⊂BCA∩B=ϕDA∪Bif set A and B are defined as A={(x,y):y=ex,x∈R}
B={(x,y):y=x,x∈R}.thenAB⊂ABA⊂BCA∩B=ϕDA∪BLet A={(x,y):y=ex,x∈R}B={(x,y),Y=e−x,x∈R}then
AA∩B=ϕBA∩B≠ϕCA∪B=R2Dnone of these
If the sets A and B are defined are defined as A={(x,y):y=ex,x∈R},B={(x,y):y=x,x∈R}then
View SolutionIn some question of sets, we have to make the use of graphs
For example
A={(x,y):y=ex,x∈R}
B={{x,y}:y=−x.x∈R}
Find n(A∩B)
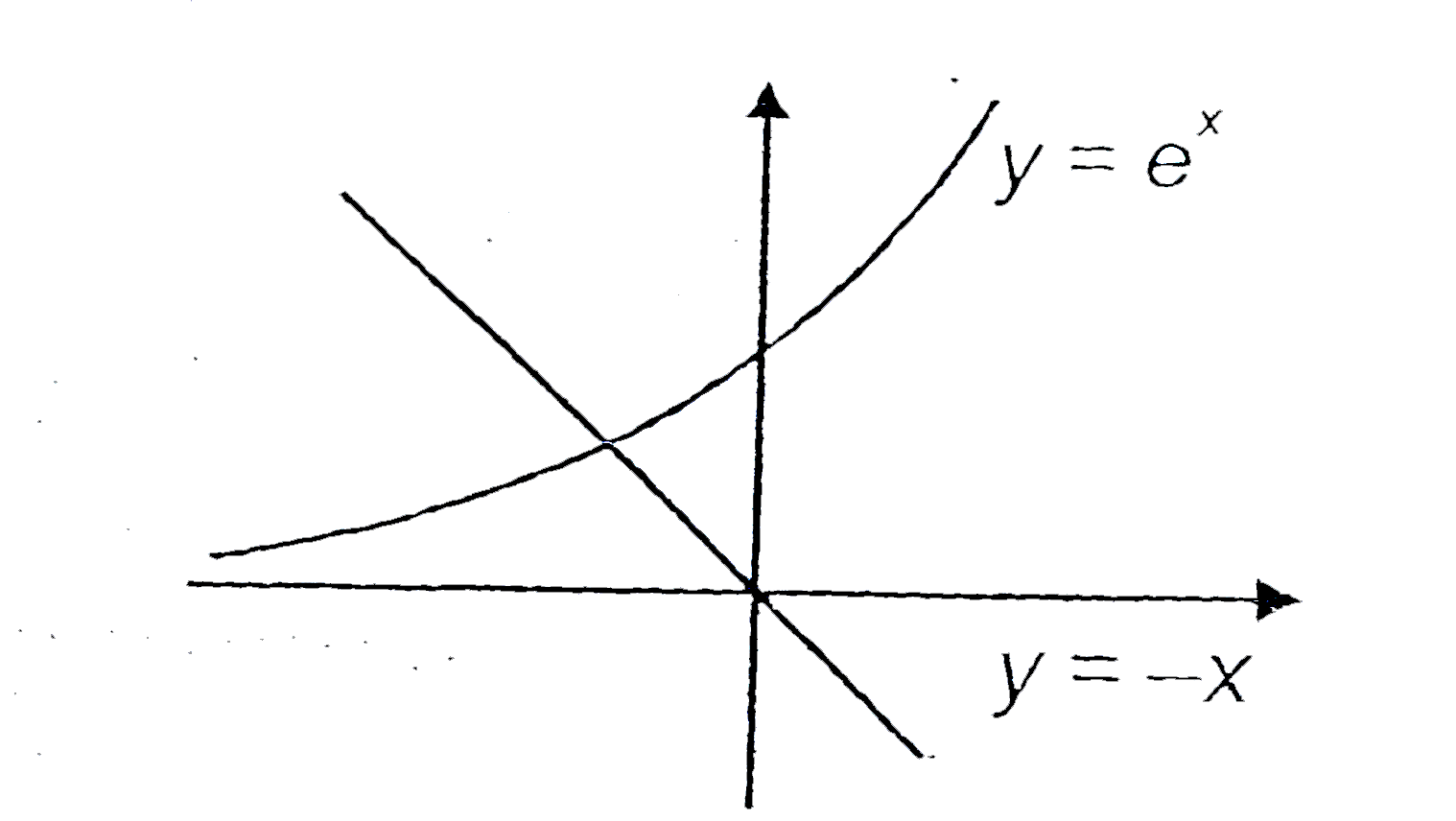
It is clear that y=exandy=−x intersect at one pont. Hence n(A∩B)=1
A={(x,y):x2+y2≤2,x,y∈R}
B={{x,y):y≥x2,x,y∈R}
Then domain of A∩B is
View SolutionIn some question of sets, we have to make the use of graphs
For example
A={(x,y):y=ex,x∈R}
B={{x,y}:y=−x.x∈R}
Find n(A∩B)
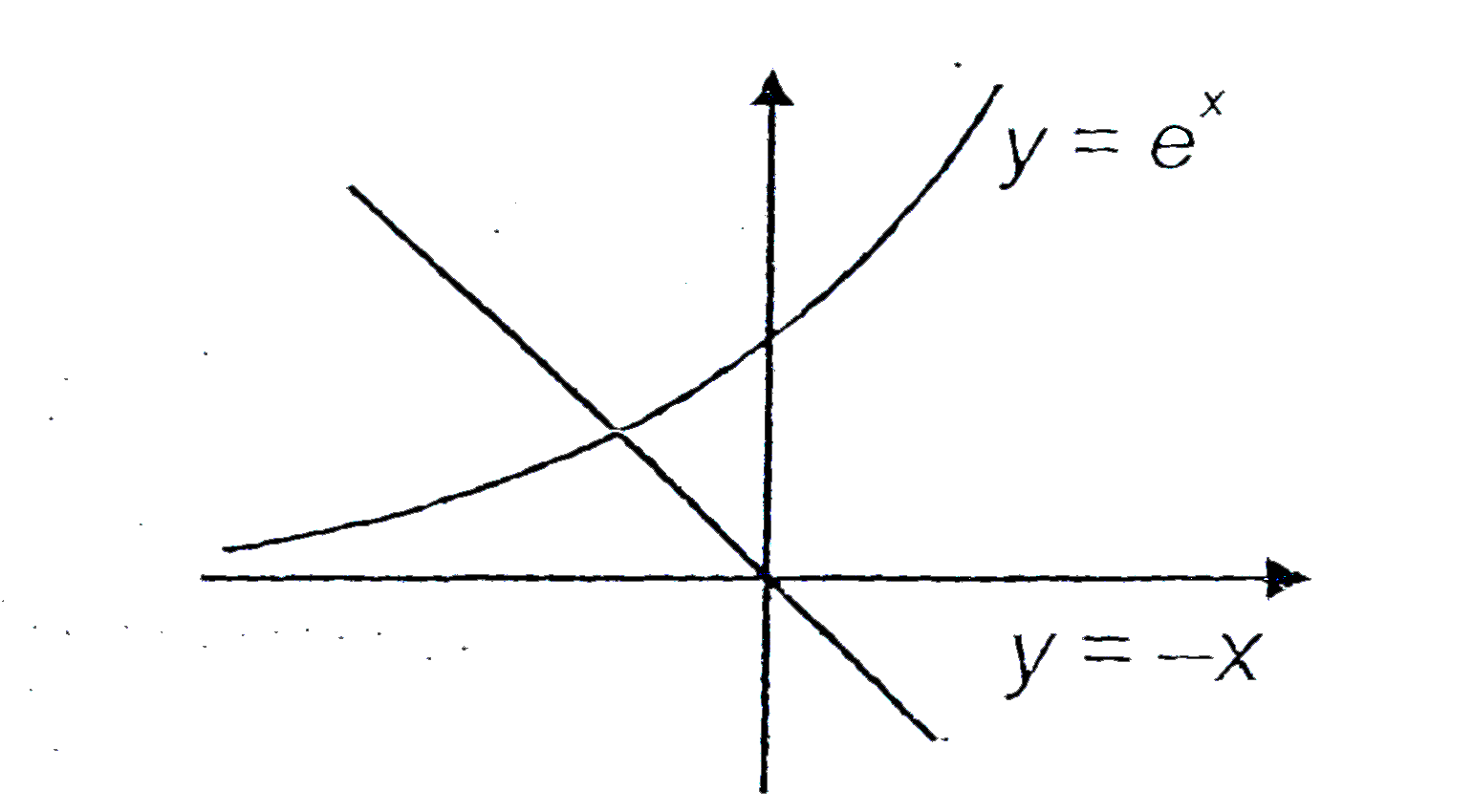
It is clear that y=exandy=−x intersect at one pont. Hence n(A∩B)=1
A={(x,y):y=sinπx,x∈R}
B={(x,y):y=|In|x||,x∈R−{0}}
Then, n(A∩B)
View SolutionIn some question of sets, we have to make the use of graphs
For example
A={(x,y):y=ex,x∈R}
B={{x,y}:y=−x.x∈R}
Find n(A∩B)
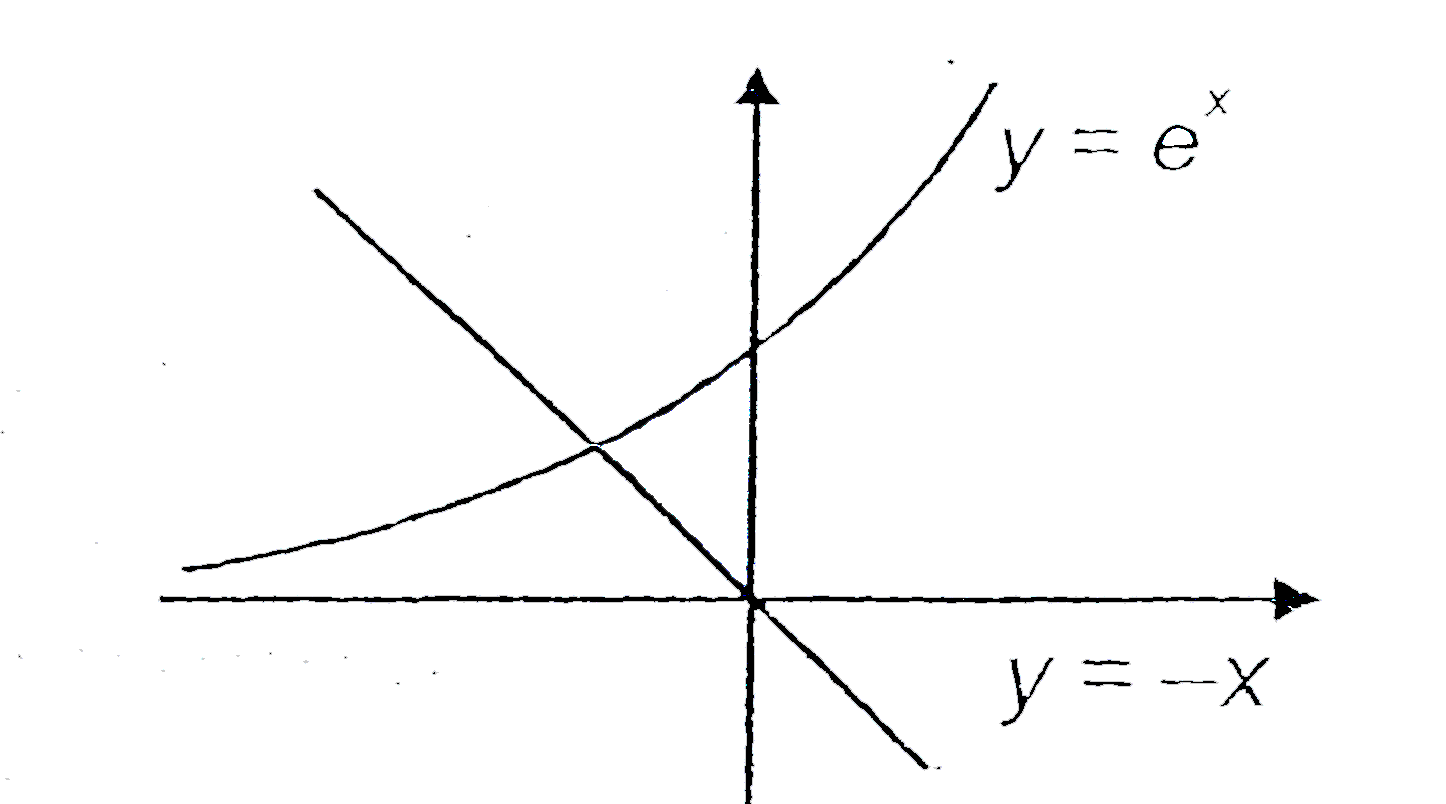
It is clear that y=exandy=−x intersect at one pont. Hence n(A∩B)=1
A:{(x,y):y=√4−x2,x∈[−2,2]}
B={(x,y):y=|x|,x∈R}
Then n(A∩B)
View SolutionIf A={(x,y}: y=3x,y∈R} and B={{x,y}:y=x,x,y∈R} then which of the following is true?
View Solution
