Two cells of emfs E1 and (E2(E1>E2) are connected as shows in Fig. 6.45.
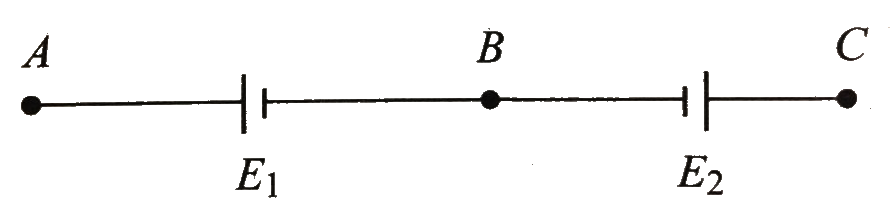
When a potentiometer is connected between A and B, the balancing length of the potentiometer wire is 300cm. On connecting the same potentiometer between A and C, the balancing length is 100cm. The ratio E1/E2 is
3:1
1:3
2:3
3:2
The correct Answer is:D
When potentiometer is connected between A and B, then it measures only E1 and when connected between A and C, then it measures E1−E2
∴E1E1−E2=l1l2
or E1−E2E1=l2l1 or 1−E2E1=100300
⇒E2E1=1−13⇒E2E1=23
⇒E1E2=32
Topper's Solved these Questions
Similar Questions
Two cells of emf E1 and E2(E1>E2) are connected as shown in the figure below. When a potentiometer is used to measure potential difference between the points A and B, the balancing length of the potentiometer wire is 300 cm. But the same potentiometer for the potential difference between points A and C, gives the balancing length 100 cm. Find E1E2.
 View Solution
View SolutionTwo primary cells of emfs E1 and E2 are connected to the potentiometer wire AB as shown in the figure . If the balancing lengths for the two combinations of the cells are 250 cm and 400 cm , find the ratio of E1 and E2 .
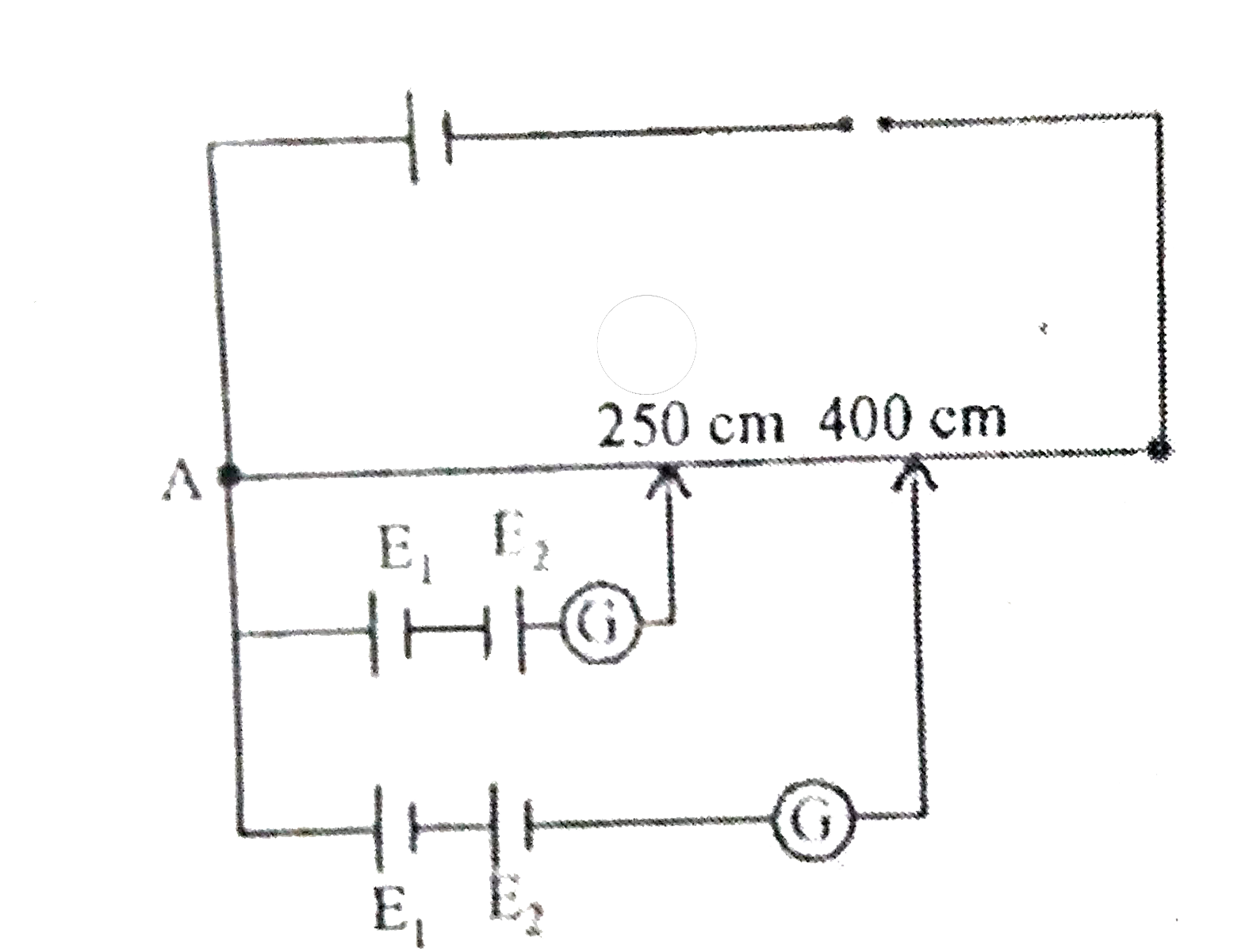 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
Two cells of emf ε1 and ε2(ε2<ε1) are joined as shown in figure :

When a potentiometer is connected between X and Y it balances for 300 cm length against ε0. On conntecting the same potentiometer between X and Z it balances for 100 cm length against ε1 and ε2. Then the ratio ε2ε1 is :A13B34C14D23 - Question 2 - Select One
Tow cells of emf E1 and E2(E1>E2) are connected individually to a potentiometer and their corresponding balancing length are 625 cm and 500 cm, then the ratio E1E2 is .
A5:4B3:1C5:1D4:5 - Question 3 - Select One
Two cells of E.M.F. E1 and E2(E2>E1) are connected in series in the secondary circuit of a potentiometer experiment for determination of E.M.F. The balancing length is found to be 825 cm. Now when the terminals to cell E1 are reversed, then the balancing length is found to be 225 cm. The ratio of E1 and E2 is
A2:3B4:7C7:4Dnone of these
A cell is balanced at 100cm of a potentiometer wire when the total length of the wire is 400cm .If the length of the potentiometer wire is increased by 100cm ,then the new balancing length for the cell will be
View SolutionTow cells of e.m.f E1 and E2 are joined in series and the balancing length of the potentiometer wire is 625 cm. If the terminals of E1 are reversed , the balancing length obtained is 125 cm. Given E2>E1,the ratio E1:E2 willbe
View SolutionTwo cells of emf E1 and E2(E1>E2) are connected in series to potentiometer for balancing length 625 cm . When polarity of E2 is reversed then balancing length becomes 125 cm. Then the ratio E1E2 is
View SolutionIn a potentiometer experiment the balancing length is 8 m, when the two cells E1 and E2 are joined in series. When the two cells are connected in opposition the balancing length is 4m. The ratio of the e.m.f. of two cells (E1/C2) is
View SolutionA cell of emf E and internal resistance r connected in the secondary gets balanced against length l of potentiometer wire. If a resistance R is connected in parallel with the cell, then the new balancing length for the cell will be
View Solution

