Find ratio of acceleration due to gravity g at depth d and at height h

Which of the following graphs shows the variation of acceleration due to gravity g with depth h from the surface of the earth ?

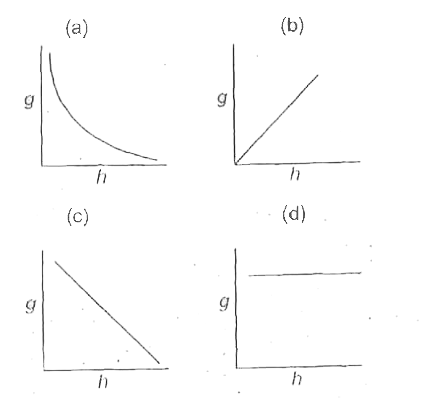A(a)
B(b)
C(c )
D(d)
At what depth below the surface of earth, value of acceleration due to gravity is same as the value at height $h = R$ , where R is the radius of earth.
A $d = \frac{R}{2}$
B $d = \frac{R}{4}$
C $d = \frac{3}{2} R$
D $d = \frac{3}{4} R$
The ratio $\frac{g}{g_{h}}$ , where g and $g_{h}$ are the acceleration due to gravity at the surface of the earth and at a height h above the earth's surface respectively, is :
A ${(1 + \frac{h}{R})}^{2}$
B ${(1 + \frac{R}{h})}^{2}$
C ${(\frac{R}{h})}^{2}$
D ${(\frac{h}{R})}^{2}$

Find ratio of acceleration due to gravity $g$ at depth $d$ and at height $h$ where $d = 2 h$