A five digit number is chosen at random. The probability that all the digits are distinct and digits at odd places are odd and digits at even places are even, is
160
275
150
175
The correct Answer is:D
Total number of 5 digit number
9×10×10×10×10=90000
Number of favourable numbers
=5×5×4×4×3=1200
Thus, required probability =120090000
=175
Topper's Solved these Questions
Similar Questions
Knowledge Check
A three digits numbre was chosen at random. Find the probability that it's hundreds digit, tens digit and units digit are consecutive integers in descending order.
A175B4225C2225D145A five digit number if formed by the digits 1,2,3,4,5,6 and 8. The probability that the number has even digit at both ends is
A37B47C27Dnone of theseA five digit number if formed by the digits 1,2,3,4,5,6 and 8. The probability that the number has even digit at both ends is
A2/7B3/7C4/7Dnone
The number of 6 digit numbers that can be made with the digits 0,1,2,3,4 and 5 so that even digits occupy odd places is
View SolutionIn a five digit number, the digit at the hundreds place is three fourth of the digit at ten thousands place and the digit at ten place is two third of the digit at hundreds place. The digit at tens place is square of the smallest prime number and the digit at thousands place is the largest at thousands place is the largest single digit prime number. If the digit at unit place is the largest single digit odd number, then the number is
View SolutionOn one page of a directory, there are 160 telephone numbers. The frequency distribution of the unit place digit is given below:
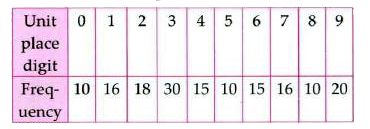
From this page, one of the numbers is chosen at random. What is the probability that the unit place digit in the chosen number is an odd prime number?
View SolutionFive digit numbers are formed such that either all the digits are even or all the digits are odd. If no digit is allowed to be repeated in one number find the difference between the maximum possible. number with odd-digits and the minimum possible number with even digits
View SolutionHow many three digit numbers are there in which all the digits are odd?
View Solution
