Let P = (-1, 0), Q = (0, 0) and R = (3, $3 \sqrt{3}$ ) be three points. The equation of the bisector of the angle PQR

A

$y = \sqrt{3} x$

B

$\sqrt{3} y = x$

C

$y = - \sqrt{3} x$

D

$\sqrt{3} y = - x$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:C

Given P = (-1,0) O = (0,0) and Q = $(3, 3 \sqrt{3})$
Equation of line OP is
$\frac{y}{x} = \frac{0}{- 1 - 0} \Rightarrow y = 0$

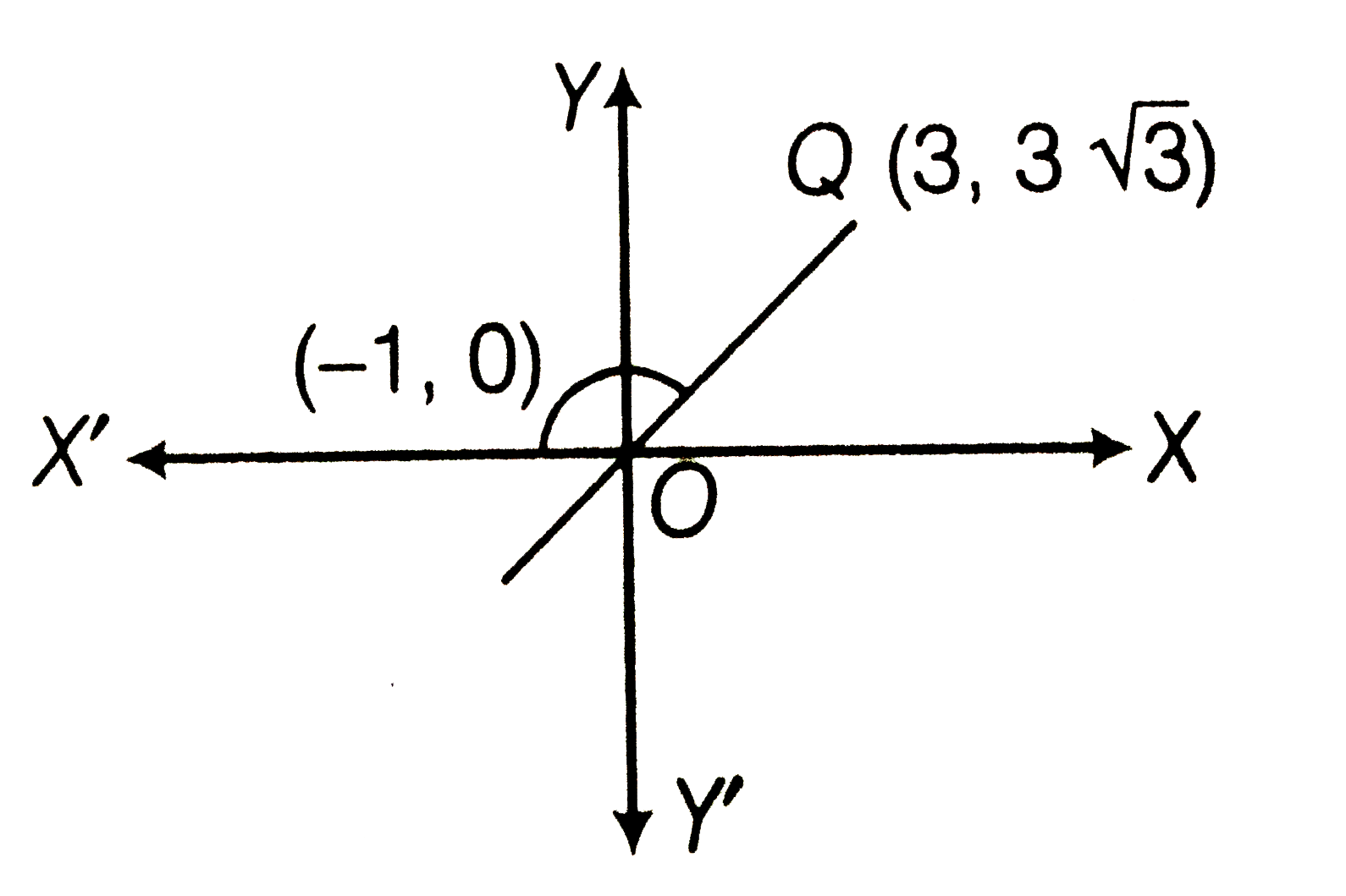
nad equation of line OQ is
$\frac{y}{x} = \frac{3 \sqrt{3} - 0}{3 - 0}$
$\Rightarrow y = \sqrt{3} x$
Angle bisector of lines y = 0 and $y = \sqrt{3} x$ will be
$\frac{y}{\sqrt{1^{2} + 0^{2}} = \pm \frac{(y - \sqrt{3} x)}{\sqrt{1 + 3}}}$
$\Rightarrow y = \pm \frac{(y - \sqrt{3} x)}{2}$
$\Rightarrow y = - \sqrt{3} x or \sqrt{3} y = x$
Hence, required equation is $y = - \sqrt{3} x$

|

Updated on:21/07/2023

Class 12 MATHS STRAIGHT LINE

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
Let P = (-1,0), Q = (0,0) and $R = (3, 3 \sqrt{3})$ be three point. The equation of the bisector of the angle PQR is:
A $\frac{\sqrt{3}}{2} x + y = 0$
B $x + \sqrt{3} y = 0$
C $\sqrt{3} x + y = 0$
D $x + \frac{\sqrt{3}}{2} y = 0$
Question 2 - Select One
Let $P = (- 1, 0), Q = (0, 0)$ and $R = (3, 3 \sqrt{3})$ be three points. The equation of the bisector of the angle PQR is
A $(\sqrt{3} / 2) x + y = 0$
B $x + \sqrt{3} y = 0$
C $\sqrt{3} x + y = 0$
D $x + (\sqrt{3} / 2) y = 0$
Question 3 - Select One
Let $P = (- 1, 0), Q (0, 0)$ and $R = (3, 3 \sqrt{3})$ be three points. Then the equation of the bisector of the angle PQR is
A $(\sqrt{3} / 2) x + y = 0$
B $x + \sqrt{3} y = 0$
C $\sqrt{3} x + y = 0$
D $x + (\sqrt{3} / 2) y = 0$

MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERS-STRAIGHT LINE -EXERCISE 2(MISCELLANEOUS PROBLEMS)

Home
Ask Doubt
Profile