Let S be the sample space of the random experiment of throwing simultaneously two unbiased dice with six faces (numbered 1 to 6) and let Ek={(a,b)∈S:ab=k} for k≥1 If pk=p(Ek) for k≥1 then correct among the following, is (Eamcet 2008)
A
p1<p30<p4<p6
B
p36<p6<p2<p4
C
p1<p11<p4<p6
D
p36<p11<p6<p4
Video Solution
Text Solution
The correct Answer is:A
Given, Ek={(a,b)∈S:ab=k} for k≥1 and pk=P(Ek)
Now, E1={(1,1)}⇒p1=P(E1)⇒p1=136
⇒E2={(1,2),(2,1)}⇒p2=P(E2)⇒p2=236
⇒E4={(1,4),(4,1),(2,2)}⇒p4=P(E4)⇒p4=336
⇒E6={(1,6),(6,1),(2,3),(3,2)}
⇒p6=P(E6)⇒p6=436
and E30={(5,6),(6,5)}
⇒p30=P(E30)⇒p30=236
∴ From the above results, we get p1<p30<p4<p6
|
Updated on:21/07/2023
Topper's Solved these Questions
- BOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - PROBABILITYEXERCISE - PRACTICE EXERCISE (Exercies 2 (MISCELLANEOUS PROBLEMS))30videos
PROBABILITY
- BOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - PROBABILITYEXERCISE - Exercise 1 (TOPICAL PROBLEMS)44videos
PROBABILITY
- BOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - PRACTICE SET 24EXERCISE - Paper 2 (Mathmatics)50videos
PRACTICE SET 24
- BOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - SEQUENCES AND SERIES EXERCISE - EXERCISE 311videos
SEQUENCES AND SERIES
Similar Questions
Knowledge Check
- Question 1 - Select One
Let T(k) be the statement 1+3+5+…+(2k-1)=k2+10 Which of the following is correct ?
AT(1) is trueBT(k) is true ⇒ T (k+1) is trueCT(n) is true for all n∈NDAll above are correct - Question 2 - Select One
Let α,β and γ be the roots of the equation x3−x−1=0. If Pk=(α)k+(β)k+(γ)k,k≥1 , then which one of the following statements is not true?
AP3=P1+P2+1BP2=P4CP5=P6DP5=P3 - Question 3 - Select One
Let Pk(k=1,2,…n) be the nth root of unity. Let z=a+ibandAk=Re(z)Re(Pk)+i{lm(z)lm(Pk)} then which of the following is true
AAk lies on ellipseBAk lies on hyperbolaCIf S be the focus of locus of Ak then n∑k=1(Ak)S=naDIf S be the focus of locus of Ak then n∑k=1(AkS)2=n2(3a2−b2)
Let sk,k=1,2,3,…,100 denote the sum of the infinite geometric series whose first term is k−1⌊k and the common ratio is 1k. Then, the value of
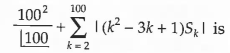 is View Solution
is View SolutionIf k,k+1,k+3 are in G.P then find the value of k
View SolutionIf k, k + 1 and k + 3 are in G.P. then find the value of k.
View SolutionLet a, b, c, d, e, be the observations with m and standard deviation s. The standard deviation of the observations a+k, b+k, c+k, d+k, e+k is s (b) ks (c) s+k (d) sk
View SolutionLet Sk, be the sum of an infinite geometric series whose first term is kand common ratio is kk+1(k>0) . Then the value of ∞∑k=1(−1)kSk is equal to
View Solution

