A lizard, at an initial distance of 21 cm behind an insect, moves from rest with an acceleration of 2cms−2 and pursues the insect which is crawling uniformly along a straight line at a speed of 20cms−1. Then the lizard will catch the insect after
24s
21s
1s
20s
The correct Answer is:B
To solve the problem, we need to find the time it takes for the lizard to catch the insect. We can use the equations of motion for both the lizard and the insect.
1. Define the Variables:
- Let the distance traveled by the lizard be s1.
- Let the distance traveled by the insect be s2.
- The initial distance between the lizard and the insect is 21 cm.
- The lizard starts from rest with an acceleration a=2cm/s2.
- The insect moves with a constant speed v=20cm/s.
2. Write the Equation for the Lizard's Motion:
- Since the lizard starts from rest, its initial velocity u=0.
- The distance traveled by the lizard after time t is given by the equation:
s1=ut+12at2=0+12⋅2⋅t2=t2
3. Write the Equation for the Insect's Motion:
- The distance traveled by the insect after time t is given by:
s2=vt=20t
4. Set Up the Equation for Catching Up:
- The lizard catches the insect when the distance it has traveled equals the distance traveled by the insect plus the initial distance of 21 cm:
s1=s2+21
- Substituting the expressions for s1 and s2:
t2=20t+21
5. Rearranging the Equation:
- Rearranging gives us:
t2−20t−21=0
6. Solving the Quadratic Equation:
- We can use the quadratic formula t=−b±√b2−4ac2a where a=1,b=−20,c=−21:
t=20±√(−20)2−4⋅1⋅(−21)2⋅1
t=20±√400+842
t=20±√4842
t=20±222
7. Calculating the Roots:
- The two possible solutions for t are:
t=422=21andt=−22=−1
- Since time cannot be negative, we discard t=−1.
8. Final Answer:
- Therefore, the lizard will catch the insect after t=21 seconds.
- Let the distance traveled by the lizard be s1.
- Let the distance traveled by the insect be s2.
- The initial distance between the lizard and the insect is 21 cm.
- The lizard starts from rest with an acceleration a=2cm/s2.
- The insect moves with a constant speed v=20cm/s.
- Since the lizard starts from rest, its initial velocity u=0.
- The distance traveled by the lizard after time t is given by the equation:
s1=ut+12at2=0+12⋅2⋅t2=t2
- The distance traveled by the insect after time t is given by:
s2=vt=20t
- The lizard catches the insect when the distance it has traveled equals the distance traveled by the insect plus the initial distance of 21 cm:
s1=s2+21
- Substituting the expressions for s1 and s2:
t2=20t+21
- Rearranging gives us:
t2−20t−21=0
- We can use the quadratic formula t=−b±√b2−4ac2a where a=1,b=−20,c=−21:
t=20±√(−20)2−4⋅1⋅(−21)2⋅1
t=20±√400+842
t=20±√4842
t=20±222
- The two possible solutions for t are:
t=422=21andt=−22=−1
- Since time cannot be negative, we discard t=−1.
- Therefore, the lizard will catch the insect after t=21 seconds.
Topper's Solved these Questions
- BOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - APPLICATIONS OF DERIVATIVESEXERCISE - MISCELLANEOUS PROBLEMS80videos
APPLICATIONS OF DERIVATIVES
- BOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - APPLICATIONS OF DERIVATIVESEXERCISE - MHT CET CORNER21videos
APPLICATIONS OF DERIVATIVES
- BOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - APPLICATIONS OF DEFINITE INTEGRALS EXERCISE - MHT CET Corner6videos
APPLICATIONS OF DEFINITE INTEGRALS
- BOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - BINOMIAL DISTRIBUTIONEXERCISE - MHT CET Corner6videos
BINOMIAL DISTRIBUTION
Similar Questions
The acceleration after t seconds of a particle which starts from rest and moves in a straight line is (8−t5)cms2. Find the velocity of the particle when the acceleration is zero.
View SolutionA plane mirror is placed with its plane at an angle 30∘ with the y-axis. Plane of the mirror is perpendicular to the xy-plane and the length of the mirror is 3m. An insect moves along x-axis starting from a distant point, with speed 2 cm/s. The druation of the time for which the insect can see its shown image in the mirror is:
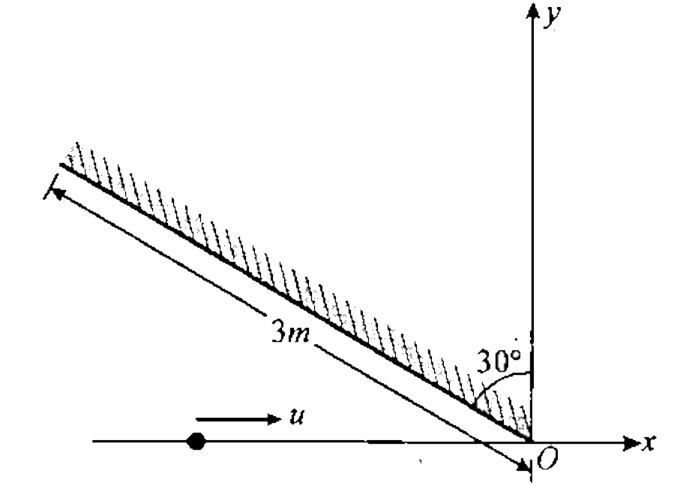 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
The displacement of a body in 8 s starting from rest with an acceleration of 20cms−2 is
A64 mB64 cmC640 cmD0.064m - Question 2 - Select One
A particle, initially at rest, starts moving in a straight line with an acceleration a=6t+4m/s2. The distance covered by it in 3 s is
A15 mB30 mC45 mD60 m - Question 3 - Select One
A bus moving along a straight line at 20 m/s undergoes an acceleration of 4 m/s2. After 2 seconds, its speed will be :
A8 m/sB12 m/sC16 m/sD28 m/s
A particle starts from the origin with a velocity of 10 and moves along a straight line. If its acceleration be (2t2−3t)cms2 at the end of t seconds, then find its velocity and the distance from the origin at the end of 6 seconds
View SolutionWhen an object is kept at a distance of 30cm from a concave mirror, the image is formed at a distance of 10 cm. If the object is moved with a speed of 9cms−1 the speed with which the image moves is
View SolutionThe ratio of distances traveled by two bodies, A and B starting form rest moving along a straight line with equal accelerations is x, where x≥1, then
View SolutionThe equation of a particle moving along a straight line is s=2t3–9t2+12t, where the units of s and t are cm and s. the acceleration of the particle will be zero after
View SolutionA particle is executing S.H.M. from mean position at 5 cm distance, acceleration is 20cm/sec2 then value of angular velocity will be
View Solution

