The maximum value of z=9x+11y subject to 3x+2y $\leq 12, 2 x + 3 y \leq 12, x \geq 0, y \geq 0$ is

A

44

B

54

C

36

D

48

Video Solution

Text Solution

Verified by Experts

The correct Answer is:D

We have, Z=9x+11y
Subject to 3x+2y $\leq 12, 2 x + 3 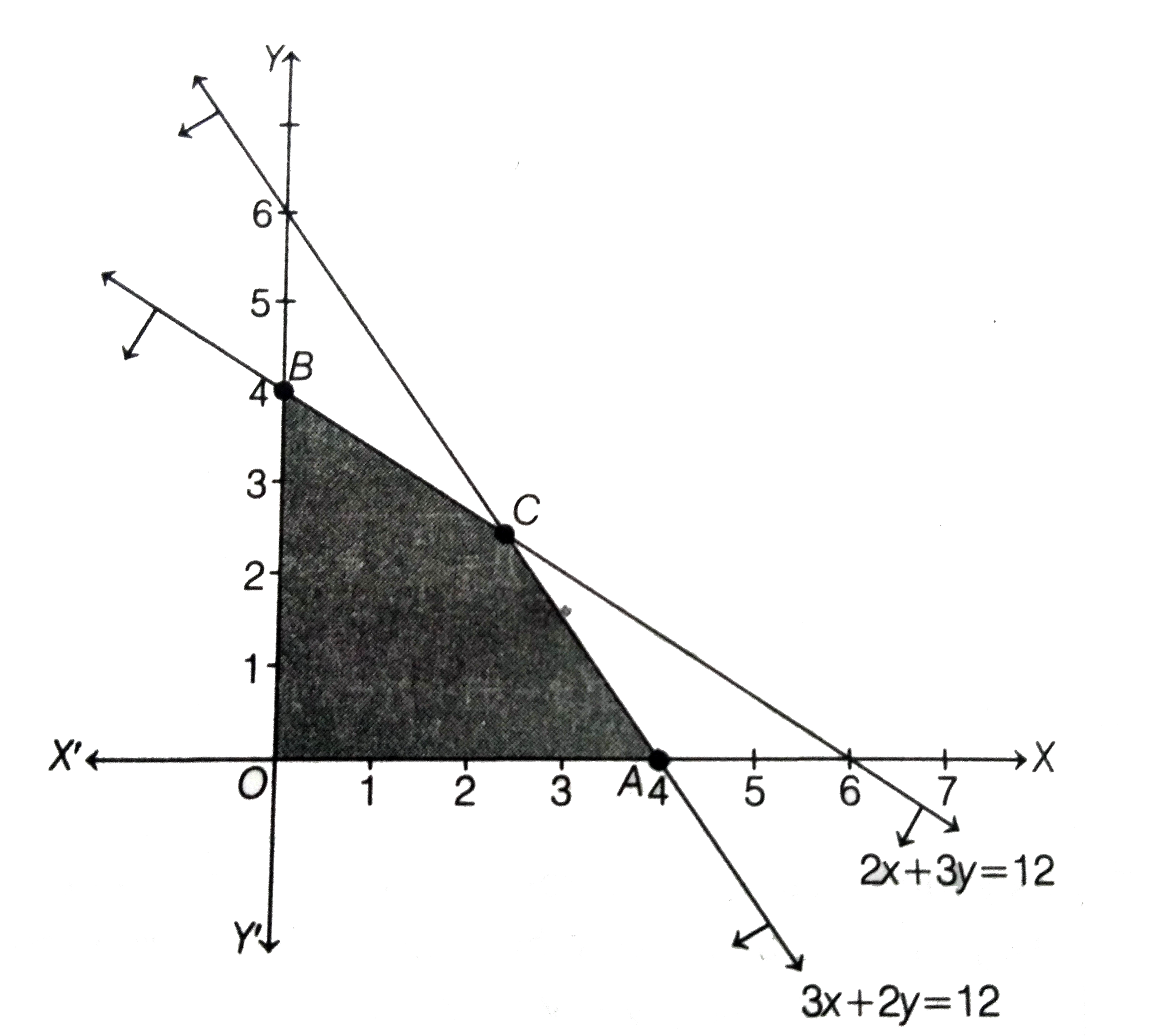y \leq 12$
Intersection point of lines 3x+2y=12 and 2x+3y=12 is $C (\frac{12}{5}, \frac{12}{5})$
Here, OACBO is the feasible region whose corner points are
O(0,0), A(4,0), C $(\frac{12}{5}, \frac{12}{5})$ and B(0,4)

|

Updated on:21/07/2023

Class 12 MATHS QUESTION BANK

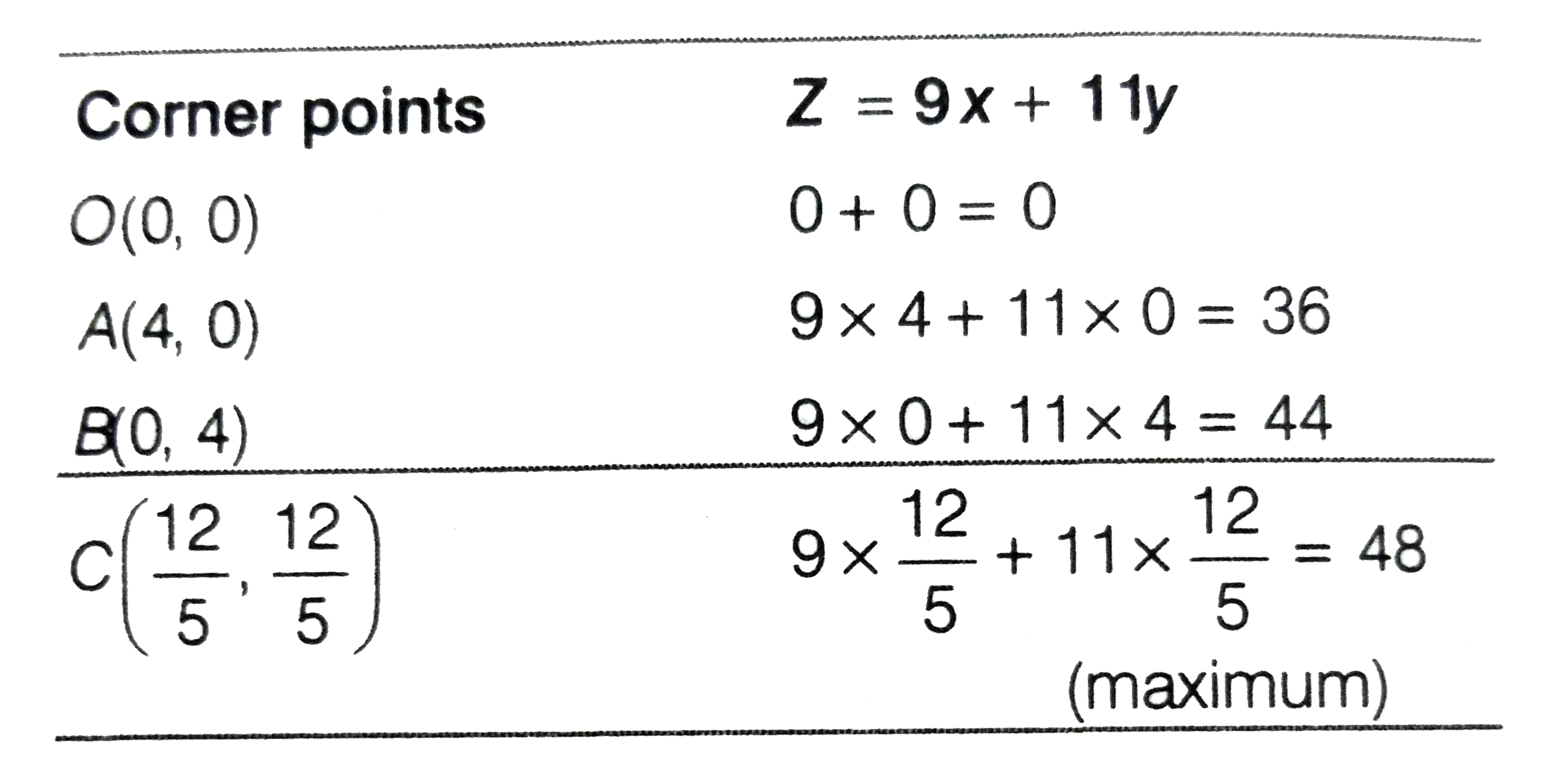
Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
The maximum value of $z = 7 x + 11 y$ subject to $3 x + 5 y \leq 26, 5 x + 3 y \leq 30, x \geq 0, y \geq 0,$ is
A42
B57.2
C61.6
D59
Question 2 - Select One
The maximum value of $z = 15 x + 30 y$ subject to $3 x + y \leq 12, x + 2 y \leq 10, x \geq 0, y \geq 0$ is
A60
B150
C160
D100
Question 3 - Select One
The maximum value of $z = 4 x + 6 y$ subject to $3 x + 2 y \leq 12, x + y \geq 4, x \geq 0, y \geq 0$ is
A36
B16
C24
D38

MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERS-SOLVED PAPER 2019-MCQS

Home
Ask Doubt
Profile