A plarinum resistance thermometer is condtructed which resds $, 0^{0}$ at ice point and $100^{0}$ at steam point. Let t $p d e \neg e t e m o e r a t u r e o n t h i s s c a \leq and \leq t t d e \neg e t h e t e m p e r a t u r e o n a m e t c u r y o n a m e r c u r y t h e m o m e n t e r s c a \leq . T h e r e s i s tan c e o f t h e p l a t \in u m c o i l v a r e s w i t h$ t $a s$ R_1 = R_0 (1+alphat + betat^2) $. D e r i v e a n exp r e s s i o n f or t h e r e s i s tan c e a s a f u n c t i o n o f$ T_p.

Video Solution

Text Solution

Verified by Experts

Let $R_{t_{p}}$ denote the residtance of the coil at the platinum scale temperature $t_{p}$ . Then
$t_{p} = \frac{R_{T_{p}} - R_{0}}{R_{100} - R_{0}} \times 100$
or, $R_{t_{p}} = \frac{t_{p}}{100} (R_{100} - R_{0}) + R_{0}$
= t_p/100 [R_0 {1+alpha xx 100 + beta xx (100)^2} - R_0] + R_0 $< b r > = \frac{t_{p}}{100} [α \times 100 + β \times {(100)}^{2}] R_{0} + R_{0}$
R_0 [ 1+ {1+{alpha xx 100 + beta xx (100)^2} t_p/100] $< b r >$ = R_0 [ 1+alphat_p + beta xx (100) t_p] $. < b r > O n l y ν m e r i c a l v a l u e s o f$ alpha and beta are to be used.

Updated on:21/07/2023

The resistance t R of a conductor varies with temperature t as shown in the figure. If the variation is represented by $R_{t} = R_{0} [1 + α t + β t^{2}]$ , then

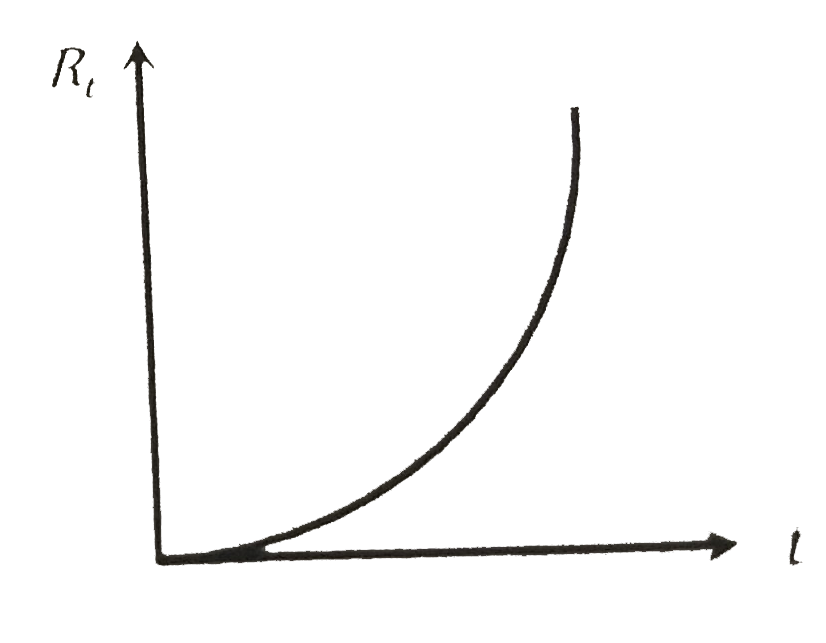A $α$ and $β$ are both negative
B $α$ and $β$ are both positive
C $α$ is positive and $β$ is negative
D $α$ is negative and $β$ are positive
Choose the most appropriate option.
The resistance R of a conductor varies with temperature t as shown in figure. If the variation is represented by $R_{t} = R_{0} (1 + α t + β t^{2})$ .

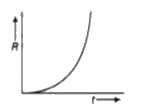
Then
A $α and β$ bothe negative
B $α$ is positive and $β$ is negative
C $α and β$ both are positive
D $α$ is negative and $β$ is negative
The charge flowing through a resistance R varies with time as $Q = 2 t - 8 t^{2}$ . The total heat produced in the resistance is (for $0 \leq t \leq \frac{1}{8})$
A $\frac{R}{6}$ joules
B $\frac{R}{3}$ joules
C $\frac{R}{2}$ joules
DR joules