Consider a triangle OAB on the xy- plane in which O is taken as origin of reference and position vector of A and B are →aand→b respectively. A line AC parallel to OB is drawn a from A. D is the mid point of OA. Now a line DC meets AB at M. Area of ΔABC is 2 times the area of ΔOAB On the basis of above information, answer the following questions 1. Position vector of point C is 2. Position vector of point M is
−−→OM=−−→OA+−−→AM
−−→OM=→a+t(→b−→a)
−−→OM=−−→OD+−−→DM
−−→OM=→a2+S(→a2+2→b)
→a+t→b−t→a=→a2+s→a2+2s→b
1−t=1+52,t=25
1=5s
s=15
−−→OM=→a+25(→b−→a)
=→a+25→b−25→a
=3→a+2→b5
Similar Questions
Let A,B,C be vertices of a triangle ABC in which B is taken as origin of reference and position vectors of A and C are →aand→c respectively. A line AR parallel to BC is drawn from A PR (P is the mid point of AB) meets AC and Q and area of triangle ACR is 2 times area of triangle ABC: (( PQ)/(QR)).((AQ)/(QC))isequal→(B)110 (C) 25 (D) 35
View SolutionLet A,B,C be vertices of a triangle ABC in which B is taken as origin of reference and position vectors of A and C are →aand→c respectively. A line AR parallel to BC is drawn from A PR (P is the mid point of AB) meets AC and Q and area of triangle ACR is 2 times area of triangle ABC: (( PQ)/(QR)).((AQ)/(QC))isequal→(B)110 (C) 25 (D) 35
View SolutionLet A,B,C be vertices of a triangle ABC in which B is taken as origin of reference and position vectors of A and C are →aand→c respectively. A line AR parallel to BC is drawn from A PR (P is the mid point of AB) meets AC and Q and area of triangle ACR is 2 times area of triangle ABC Positon vector of Q for position vector of R in (1) is (A) 2→a+3→c5 (B) 3→a+2→c5 (C) →a+2→c5 (D) none of these
View SolutionLet A,B,C be vertices of a triangle ABC in which B is taken as origin of reference and position vectors of A and C are →aand→c respectively. A line AR parallel to BC is drawn from A PR (P is the mid point of AB) meets AC and Q and area of triangle ACR is 2 times area of triangle ABC Positon vector of Q for position vector of R in (1) is (A) 2→a+3→c5 (B) 3→a+2→c5 (C) →a+2→c5 (D) none of these
View SolutionLet A,B,C be vertices of a triangle ABC in which B is taken as origin of reference and position vectors of A and C are →aand→c respectively. A line AR parallel to BC is drawn from A PR (P is the mid point of AB) meets AC and Q and area of triangle ACR is 2 times area of triangle ABC Position vector of R in terms →aand→c is (A) →a+2→c (B) →a+3→c (C) →a+→c (D) →a+4→c
View SolutionLet A,B,C be vertices of a triangle ABC in which B is taken as origin of reference and position vectors of A and C are →aand→c respectively. A line AR parallel to BC is drawn from A PR (P is the mid point of AB) meets AC and Q and area of triangle ACR is 2 times area of triangle ABC Position vector of R in terms →aand→c is (A) →a+2→c (B) →a+3→c (C) →a+→c (D) →a+4→c
View SolutionIf a and b are position vectors of A and B respectively the position vector of a point C on AB produced such that −−→AC=3−−→AB is
View Solution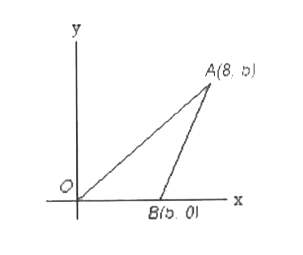
In the xy - plane above, the area of triangle OAB is 32. What is the value of b?
View SolutionIf a and b are position vectors of A and B respectively the position vector of a point C on AB produced such that −−→AC=3−−→AB is
View SolutionIf →a, →b, →c are position vectors o the point A, B, and C respectively, write the value of →AB+→BC+→AC.
View Solution
