OAB is a given triangle such that −−→OA=→a,−−→OB=→b. Also C is a point on −−→AB such that −−→AB=2−−→BC. What is −−→AC equal to ?
12(→b−→a)
12(→b+→a)
32(→a−→b)
32(→b−→a)
The correct Answer is:A
In ΔOAB,
Let −−→OA=→a
−−→OB=→b
−−→OA+−−→AB=−−→OB
⇒−−→AB=−−→OB−−−→OA
=→b−→a
−−→AB=2−−→BC
⇒C is mid point of −−→AB
∴−−→AC=12−−→AB=12(→b−→a)

Topper's Solved these Questions
Similar Questions
Knowledge Check
ABCD is a parallelogram . If −−→AB=→a,−−→BC=→b, then what −−→BD equal to ?
A→a+→bB→a−→bC−→a−→bD−→a+→b→a+→b+→c=→0 such that |→a|=3,∣∣→b∣∣=5and|→c|=7.
What is ∣∣→a+→b∣∣ equal to ?A7B8C10D11If ABCDE is a pentagon, then
−−→AB+−−→AE+−−→BC+−−→DC+−−→ED+−−→AC is equal toA4−−→ACB2−−→ACC3−−→ACD5−−→AC
In a triangle ABC, if ∣∣∣−−→BC∣∣∣=8,∣∣∣−−→CA∣∣∣=7,∣∣∣−−→AB∣∣∣=10, then the projection of the −−→AB on −−→AC is equal to :
View SolutionIf →C is the midpoint of −−→ABand→P is any point outside −−→AB, then −−→PA+−−→PB=
View SolutionOrthocenter of an equilateral triangle ABC is the origin O. If −−→OA=→a,−−→OB=→b,−−→OC=→c, then −−→AB+2−−→BC+3−−→CA=
View Solution→a+→b+→c=→0 such that |→a|=3,∣∣→b∣∣=5and|→c|=7.
What is →a.→b+→b.→c+→c.→a equal to ?
View SolutionAssertion A : If A, B, C, D are four points on a semi-circular arc with centre at 'O' such that
∣∣∣−−→AB∣∣∣=∣∣∣−−→BC∣∣∣=∣∣∣−−→CD∣∣∣, then
−−→AB+−−→AC+−−→AD=4−−→AO+−−→OB+−−→OC
Reason R : Polygon law of vector addition yields
−−→AB+−−→BC+−−→CD+−−→AD=2−−→AO
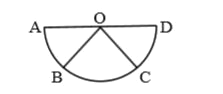
In the light of the above statements, choose the most appropriate answer from the options given below :
View Solution
