अंतराल [−√13,√13] में स्थित उन बिन्दुओ की संख्या ज्ञात करो जिन पर f(x)=sinx2+cosx2का मान अधिकतम है।
∵ f(x)=sinx2+cosx2
=√2[1√2cosx2+1√2sinx2]
√2का अंश व् हर में गुण करने पर,
=√2[cosx2cosπ4+sinπ4sinx2] [∵12=cosπ4=sinπ4
=√2[cos(x2−π4)]
।उचिष्ट मान के लिए
x2−(π)(4)=2nπ
⇒ x2=2nπ+π4
n = 0 के लिए,
x2=0+π4
⇒ x=±√π4
तथा n = 1 के लिए,
x2=2π+π4
=9π4
x=±√9π4
अर्थात f(x)[−√13,√13],में 4 बिन्दुओ पर उचिष्ट है।
Topper's Solved these Questions
Similar Questions
एक वृत की त्रिज्या r = 6 सेमी पर r के सापेक्ष क्षेत्रफल में परिवर्तन की दर है:
View Solutionनिम्नलिखित अवकल समीकरणों को हल कीजिए
2x2dy=(x2+y2)dx
View Solutionआव्यूह [0110] का क्रम होगा
View Solutionlimx→asinx−sina√x−√a का मान ज्ञात कीजिए ।
View Solutionअन्तराल ज्ञात कीजिए जिन पर
f(x)=4sinx−2x−xcosx2+cosx
से प्रदत्त फलन f (i ) निरंतर वर्धमान (ii ) निरंतर ह्रासमान है।
View Solutiona का न्यूनतम मान ज्ञात कीजिए कि फलन f(x)=x2+ax+5 अंतराल [1, 2] में वर्धमान है।
View Solutionवक्र y=√7x+2−3 पर उन बिन्दुओं को ज्ञात कीजिए जिन पर स्पर्श रेखा की प्रवणता 7 है।
View Solutionफलन y=f(x) के लिए यदि dydx=6(x−2)(x−3) है तो के ty अधिकतम मान के लिए का x मान ज्ञात कीजिये
View Solutionअंतराल (0,π2) में फलन log sin x है
View Solutionत्रिकोणमितीय समीकरण| sinx, का मान ज्ञात होने पर x का व्यापक मान ज्ञात करना
View Solutionत्रिकोणमितीय समीकरण|cosx, का मान ज्ञात होने पर x का व्यापक मान ज्ञात करना
View Solutionx का मान ज्ञात करो - 23[4x−1]−[4x−1−3x2]=x−72
View SolutionTi में 'm' के +1 और-1 मान वाले इलेक्ट्रॉनों की अधिकतम संख्या ज्ञात कीजिए।
View Solution(M) में किरेल कार्बन की संख्या =X (N) [(N) में ज्यामितीय समावयवीयों की संख्या =y] y/2 का मान है :
View SolutionX = उन यौगिकों की संख्या जिनमें -I समूह सीधे बेन्जीन से जुड़े हुए हैं।
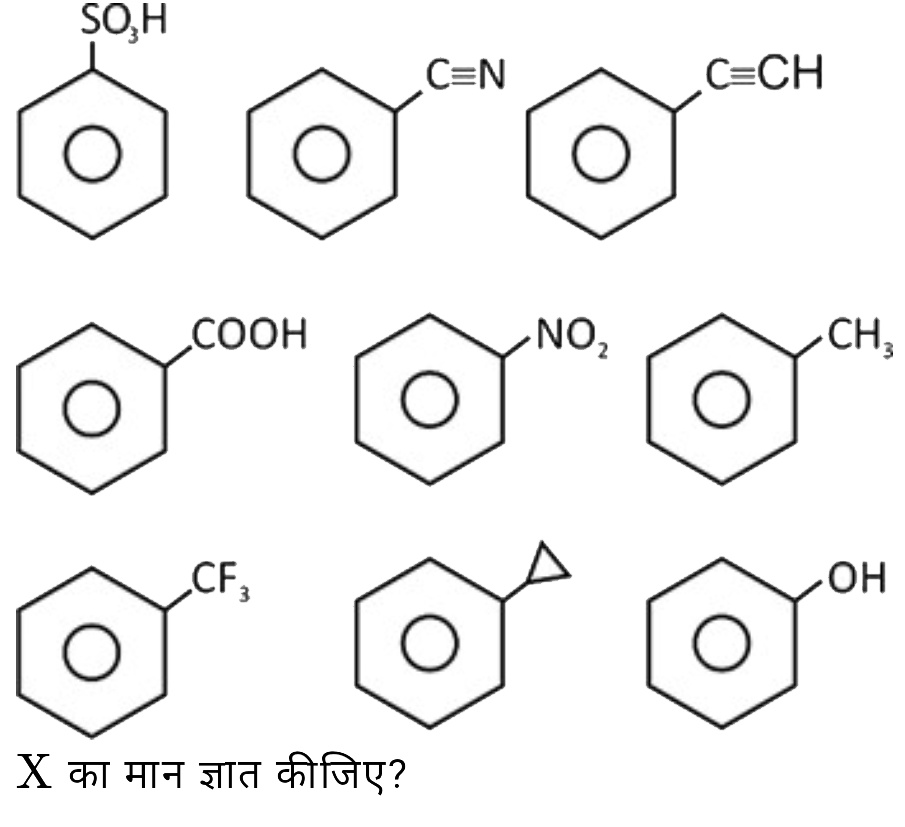
X का मान ज्ञात कीजिए?
View Solution
