बिंदु (1 ,1 ) से वक्र f(x)=x2+bx−bपर खींची गई स्पर्श रेखाओं तथा अक्ष के बीच जब प्रथम चतुर्थाश में स्थित है, बने त्रिभुज का क्षेत्रफल 2 मात्रक है तो b का मान ज्ञात कीजिए।
y=x2+bx−b
dydx=2x+b
बिंदु (1 ,1 ) पर dydx=2+b
बिंदु (1 ,1 ) पर स्पर्श रेखा का समीकरण
y−1=(2+b)(x−1)
अक्षो पर y = 0 से अन्तःखण्ड
A=1−12+b=b+1b+2
तथा B=1−(2+b)=−(b+1)
Δ का क्षेत्रफल =12AB=2
⇒ AB=4
∴ −(b+1)(b+1)=4(b+2)
⇒ b2+6b+9=0
⇒ (b+3)2=0
⇒ b=−3
Topper's Solved these Questions
Similar Questions
एक वृत की त्रिज्या r = 6 सेमी पर r के सापेक्ष क्षेत्रफल में परिवर्तन की दर है:
View Solutionनिम्नलिखित अवकल समीकरणों को हल कीजिए
2x2dy=(x2+y2)dx
View Solutionआव्यूह [0110] का क्रम होगा
View Solutionउस सरल रेखा का समीकरण ज्ञात कीजिए जो बिंदु(1,2) से होकर जाती है जिसके द्वारा अक्षो से बने त्रिभुज का क्षेत्रफल 92 वर्ग इकाई है
View Solutionबिंदु A(−2,−4)से होकर जाने वाली रेखा X-अक्ष के साथ45∘ का कोण बनाती है तथा रेखा x+3y=8 को बिंदु P पर काटती है AP, के बीच कि दूरी ज्ञात कीजिए ।
View Solutionएक रेखा X- अक्ष तथा Y-अक्ष को बिंदु A तथा B पर मिलती है AB का मध्य बिंदु (x1,y1) है तो रेखा का समीकरण है -
View Solutionदी गई आकृति में बिंदु B ,C तथा D से गुजरने वाले वृत्त के बिंदु B तथा C पर AB तथा AC स्पर्श रेखाएं है। यदि ∠BAC=70∘ और ∠CBD=90∘ तो ∠BCD का मान है -
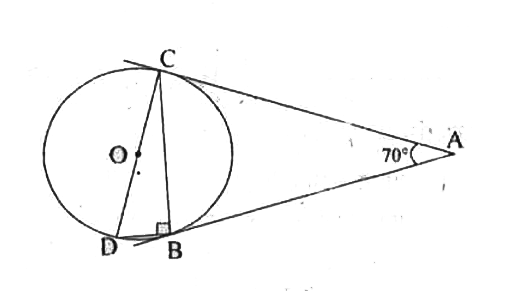
View Solutionवक्र y=logx,x− अक्ष और x = 2 के बीच का क्षेत्रफल है :
View Solutionदो स्थिर बिंदुओं A और B के निर्देशांक क्रमश :(5,3) और (3,−2) है । बिंदु P इस प्रकार गमन करता है कि त्रिभुज PAB का क्षेत्रफल 9 वर्ग क्षेत्रफल वर्ग मात्रक रहता है । बिंदु P का बिन्दुपथ ज्ञात कीजिए ।
View Solutionप्रथम चतुर्थांश में रेखाओं x = a, y = a तथा x2+y2=a2 से घिरे क्षेत्र का क्षेत्रफल ज्ञात कीजिए।
View Solutionयदि वक्र y2=ax3+b के बिंदु (2,30 पर खींची गई स्पर्श रेखा का झुकाव 4 हो, तो a का मान लिखिए
View Solutionकिसी वृत्त की जीवा AB द्वारा केंद्र पर अंतरित कोण 140∘ है तो A तथा B बिन्दुओ पर खींची गयी स्पर्श रेखाओ के बीच का कोण ज्ञात कीजिए।
View Solutionवृत्त के बाहर स्थित बिंदु से खींची गई स्पर्श रेखाओं की संख्या हो सकती है:
View Solutionकिसी वृत्त की जीवा AB द्वारा केंद्र पर अंतरित कोण 140∘ है तो A तथा B बिन्दुओ पर खींची गयी स्पर्श रेखाओ के बीच का कोण ज्ञात कीजिए।
View Solutionवृत्त x2+y2=4 के बिंदु (√3,1) पर खींची गई स्पर्श रेखा और अभिलम्ब तथा X-अक्ष एक त्रिभुज बनाते है । इस त्रिभुज का (वर्ग इकाइयो में) क्षेत्रफल है
View Solutionदीर्घवृत्त 3x2+5y2=32 के बिंदु P (2,2) पर खींची गई स्पर्श रेखा तथा अभिलम्ब, X-अक्ष को क्रमश: Q तथा R पर काटते है, तो ΔPQR का क्षेत्रफल (वर्ग इकाइयो में) है
View Solution
