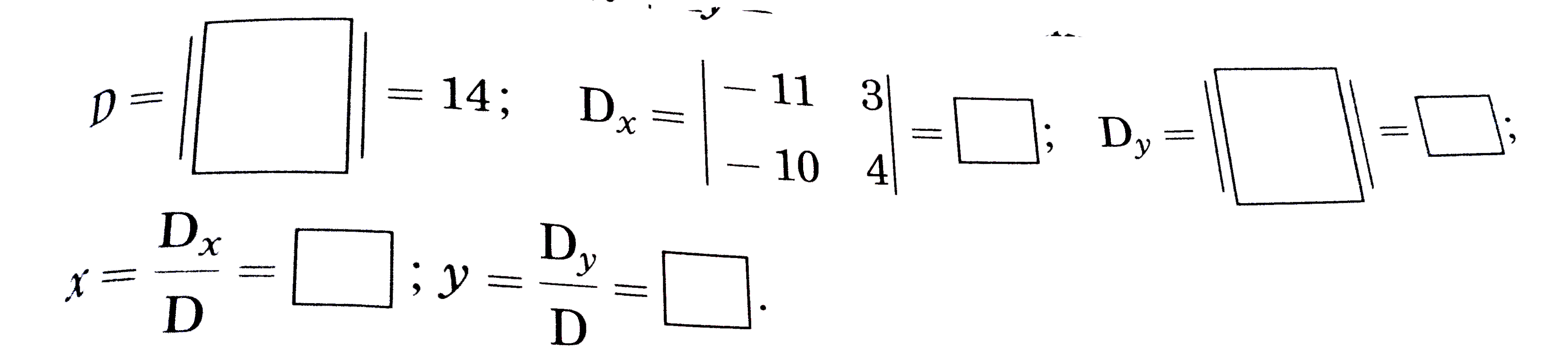Solve the simultaneous equations 3x−y=7, x+4y=11 using Cramer's rule.
To solve the simultaneous equations 3x−y=7 and x+4y=11 using Cramer's rule, we will follow these steps:
Step 1: Write the equations in standard form
The given equations are already in standard form:
1. 3x−y=7
2. x+4y=11
Step 2: Identify coefficients
From the equations, we can identify the coefficients:
- For the first equation: a1=3, b1=−1, c1=7
- For the second equation: a2=1, b2=4, c2=11
Step 3: Calculate the determinant D
The determinant D is calculated using the formula:
D=a1b2−a2b1
Substituting the values:
D=(3)(4)−(1)(−1)=12+1=13
Step 4: Calculate Dx
To find Dx, we replace the first column of the coefficient matrix with the constants from the right side of the equations:
Dx=∣∣∣7−1114∣∣∣
Calculating Dx:
Dx=(7)(4)−(11)(−1)=28+11=39
Step 5: Calculate Dy
To find Dy, we replace the second column of the coefficient matrix with the constants:
Dy=∣∣∣37111∣∣∣
Calculating Dy:
Dy=(3)(11)−(1)(7)=33−7=26
Step 6: Calculate x and y
Using Cramer’s rule:
x=DxD=3913=3
y=DyD=2613=2
Final Solution
The solution to the simultaneous equations is:
x=3,y=2
---
The given equations are already in standard form:
1. 3x−y=7
2. x+4y=11
From the equations, we can identify the coefficients:
- For the first equation: a1=3, b1=−1, c1=7
- For the second equation: a2=1, b2=4, c2=11
The determinant D is calculated using the formula:
D=a1b2−a2b1
Substituting the values:
D=(3)(4)−(1)(−1)=12+1=13
To find Dx, we replace the first column of the coefficient matrix with the constants from the right side of the equations:
Dx=∣∣∣7−1114∣∣∣
Calculating Dx:
Dx=(7)(4)−(11)(−1)=28+11=39
To find Dy, we replace the second column of the coefficient matrix with the constants:
Dy=∣∣∣37111∣∣∣
Calculating Dy:
Dy=(3)(11)−(1)(7)=33−7=26
Using Cramer’s rule:
x=DxD=3913=3
y=DyD=2613=2
The solution to the simultaneous equations is:
x=3,y=2
Topper's Solved these Questions
- BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - LINEAR EQUATIONS IN TWO VARIABLESEXERCISE - Assignment 1.49videos
LINEAR EQUATIONS IN TWO VARIABLES
- BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - LINEAR EQUATIONS IN TWO VARIABLESEXERCISE - Practice set 1.19videos
LINEAR EQUATIONS IN TWO VARIABLES
- BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - LINEAR EQUATIONS IN TWO VARIABLESEXERCISE - Assignment 1.310videos
LINEAR EQUATIONS IN TWO VARIABLES
- BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - GEOMETRIC CONSTRUCTIONS EXERCISE - CHALLENGING QUESTION4videos
GEOMETRIC CONSTRUCTIONS
- BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - MENSURATIONEXERCISE - Assignment 8.58videos
MENSURATION
Similar Questions
Knowledge Check
- Question 1 - Select One
Solve the simultaneous equations:
2x-3y = 11 and 5x + 4y =16Ax=5,y=−13Bx=2,y=23Cx=-1, y = 4Dx=4,y=−1
What is the value of Dx, for solving the simultaneous equations 3x+2y=11 and 7x−4y=9 by Cramer's rule ?
View SolutionWhat is the value of Dy , for solving the simultaneous equations 3x+y=1 and 2x−11y=3 by Cramer's rule?
View SolutionSolve the simultaneous equations x+y=7,2x−3y=9 by Cramer's method
View SolutionSolve the following simultaneous equations by using Cramer's rule:
3x+y=1,2x−11y=3View SolutionSolve the following simultaneous equations using Cramer's rule .
x+2y=−1,2x−3y=12View SolutionSolve the simultaneous equations :
4x+5y=7,3x+4y=5View SolutionSolve the simultaneous equations using Cramer's rule x+2y=−1,2x−3y=12
View Solution