A person of mass M is setting on a swing of length L and swinging with an angular amplitude θ0 if the person stands up when the swing passes through its lowest point, the work done by him, assuming that his centre of mass moves by a distance l(<<L)
Mgl(1−θ0)2
Mgl(1+hη20)
Mgl
Mgl(1+θ202)
The correct Answer is:A
To solve the problem, we need to analyze the situation step by step. The person is sitting on a swing of length L and swings with an angular amplitude θ0. When the swing passes through its lowest point, the person stands up, and we need to find the work done by the person, assuming that his center of mass moves a distance l (where l≪L).
1. Identify the Initial Conditions:
- The person has a mass M.
- The swing has a length L.
- The angular amplitude is θ0.
- The swing passes through its lowest point with maximum speed v0.
2. Determine the Initial Angular Momentum:
- At the lowest point, the angular momentum Li about the point of suspension is given by:
Li=M⋅v0⋅L
3. Determine the Final Angular Momentum:
- After the person stands up, the new speed v1 can be expressed in terms of the distance moved by the center of mass:
Lf=M⋅v1⋅(L−l)
- By conservation of angular momentum, we have:
M⋅v0⋅L=M⋅v1⋅(L−l)
- Simplifying gives:
v1=v0⋅LL−l
4. Apply the Work-Energy Theorem:
- The change in kinetic energy is equal to the work done on the person:
ΔKE=KEf−KEi
- This can be expressed as:
ΔKE=12Mv21−12Mv20
5. Substituting for v1:
- Substitute v1 into the kinetic energy equation:
ΔKE=12M(v0LL−l)2−12Mv20
6. Calculate the Work Done by Gravity:
- The work done by gravity when the center of mass moves a distance l is:
Wg=Mgl
7. Set Up the Equation:
- According to the work-energy theorem:
ΔKE=Wperson+Wg
- Rearranging gives:
Wperson=ΔKE−Wg
8. Substituting Values:
- Substitute the expressions for ΔKE and Wg into the equation to find Wperson.
9. Final Expression:
- After simplification and applying the binomial approximation for l≪L, we arrive at:
Wperson=Mgl(1+θ20)
Final Answer:
The work done by the person when he stands up is:
Wperson=Mgl(1+θ20)
- The person has a mass M.
- The swing has a length L.
- The angular amplitude is θ0.
- The swing passes through its lowest point with maximum speed v0.
- At the lowest point, the angular momentum Li about the point of suspension is given by:
Li=M⋅v0⋅L
- After the person stands up, the new speed v1 can be expressed in terms of the distance moved by the center of mass:
Lf=M⋅v1⋅(L−l)
- By conservation of angular momentum, we have:
M⋅v0⋅L=M⋅v1⋅(L−l)
- Simplifying gives:
v1=v0⋅LL−l
- The change in kinetic energy is equal to the work done on the person:
ΔKE=KEf−KEi
- This can be expressed as:
ΔKE=12Mv21−12Mv20
- Substitute v1 into the kinetic energy equation:
ΔKE=12M(v0LL−l)2−12Mv20
- The work done by gravity when the center of mass moves a distance l is:
Wg=Mgl
- According to the work-energy theorem:
ΔKE=Wperson+Wg
- Rearranging gives:
Wperson=ΔKE−Wg
- Substitute the expressions for ΔKE and Wg into the equation to find Wperson.
- After simplification and applying the binomial approximation for l≪L, we arrive at:
Wperson=Mgl(1+θ20)
The work done by the person when he stands up is:
Wperson=Mgl(1+θ20)
Topper's Solved these Questions
Similar Questions
A simple pendilum with bob of mass m and length l is held in position at an angle θ with t he verticle. Find its speed when it passes the lowest position.
View SolutionA simple pendulum with a bob of mass m and a conducting wire of length L, swings under gravity with an angular amplitude 2θ. If the horizontal component of the earth's magnetic field perpendicular to the plane of motion of the pendulum is B, then the maximum emf induced across the pendulum is
View Solution
Knowledge Check
A stone of mass m is tied to a string and is moved in a vertical circle of radius r making n revolution per minute. The total tension in the string when the stone is its lowest point is.
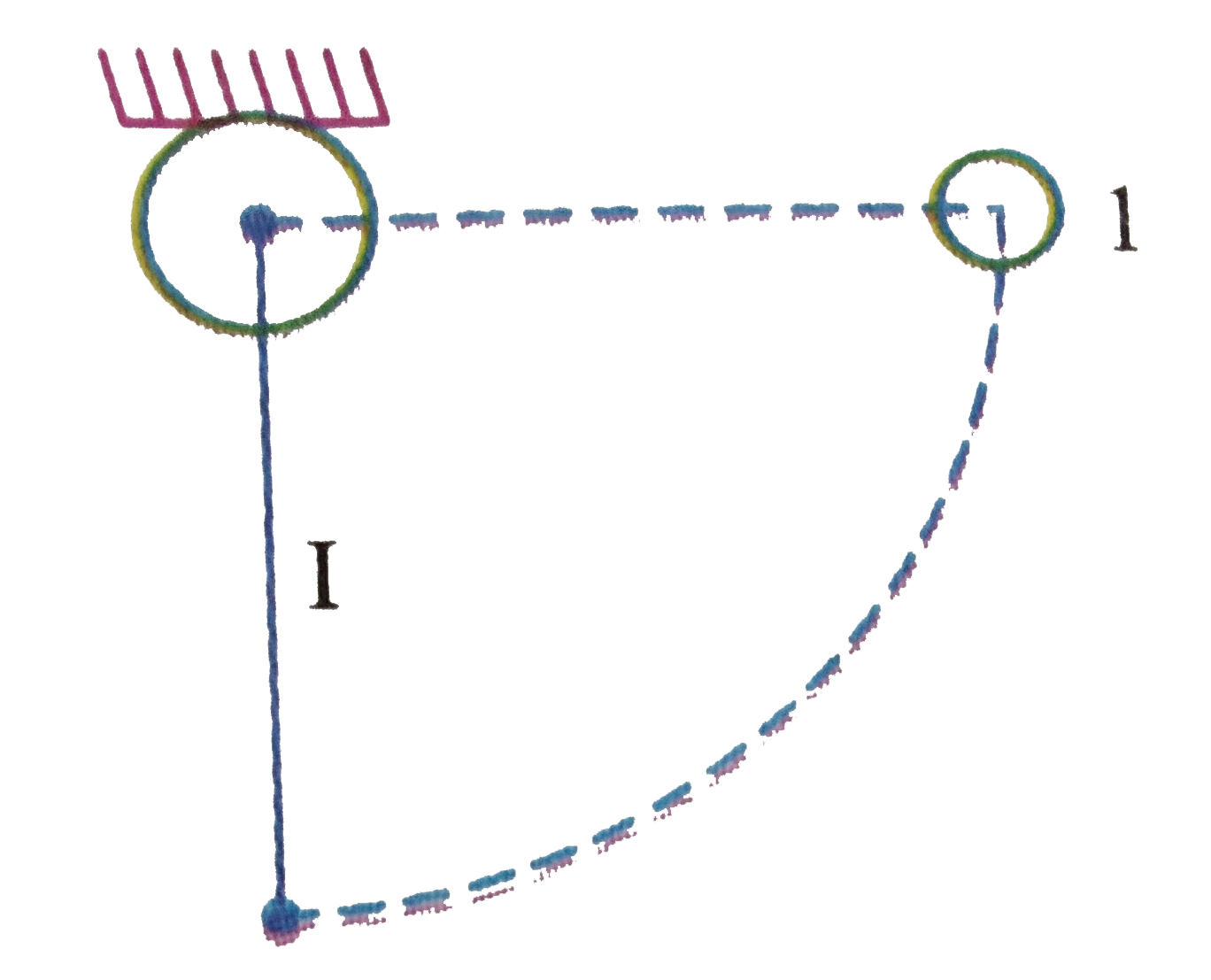
Am[g+4π2r]Bm[g+π2n2r260]Cm[g+π2n2r900]Dm[g+n2r2]A sphere of mass m attached with the free end of a steel wire of length l swings in the veritcle plane form the horizontal positon.
Elastic energy should in the wire in the vericle positon isA9m2g2l2Yπr2B7m2g2l2Yπr2C9m2g2lYπr2D9m2g2l4Yπr2A simple pendulum with a bob of mass 'm' swings with angular amplitude of 60∘. When its angular displacement is 30∘, the tension in the strings would be
A3√3mgBmg2(3√3−2)C12mg(3√3+2)D12mg(3−√2)
A child of mass m is sitting on a swing suspended by a rope of length L. The swing and the rope have negligible mass and the dimension of child can be neglected. Mother of the child pulls the swing till the rope makes an angle of θ0=1 radian with the vertical. Now the mother pushes the swing along the arc of the circle with a force F=Mg2 and releases it when the string gets vertical. How high will the swing go? [Take cos(1 radian) ≅0.5]
View SolutionA person of mass m is standing in a lift. Find his apparent weight when the lift is : moving downward with uniform acceleration a(<g)
View SolutionA simple pendulum with a bob of mass m swings with an angular amplitude of 40∘. When its angular displacement is 20∘, the tension in the string is greater than mgcos20∘
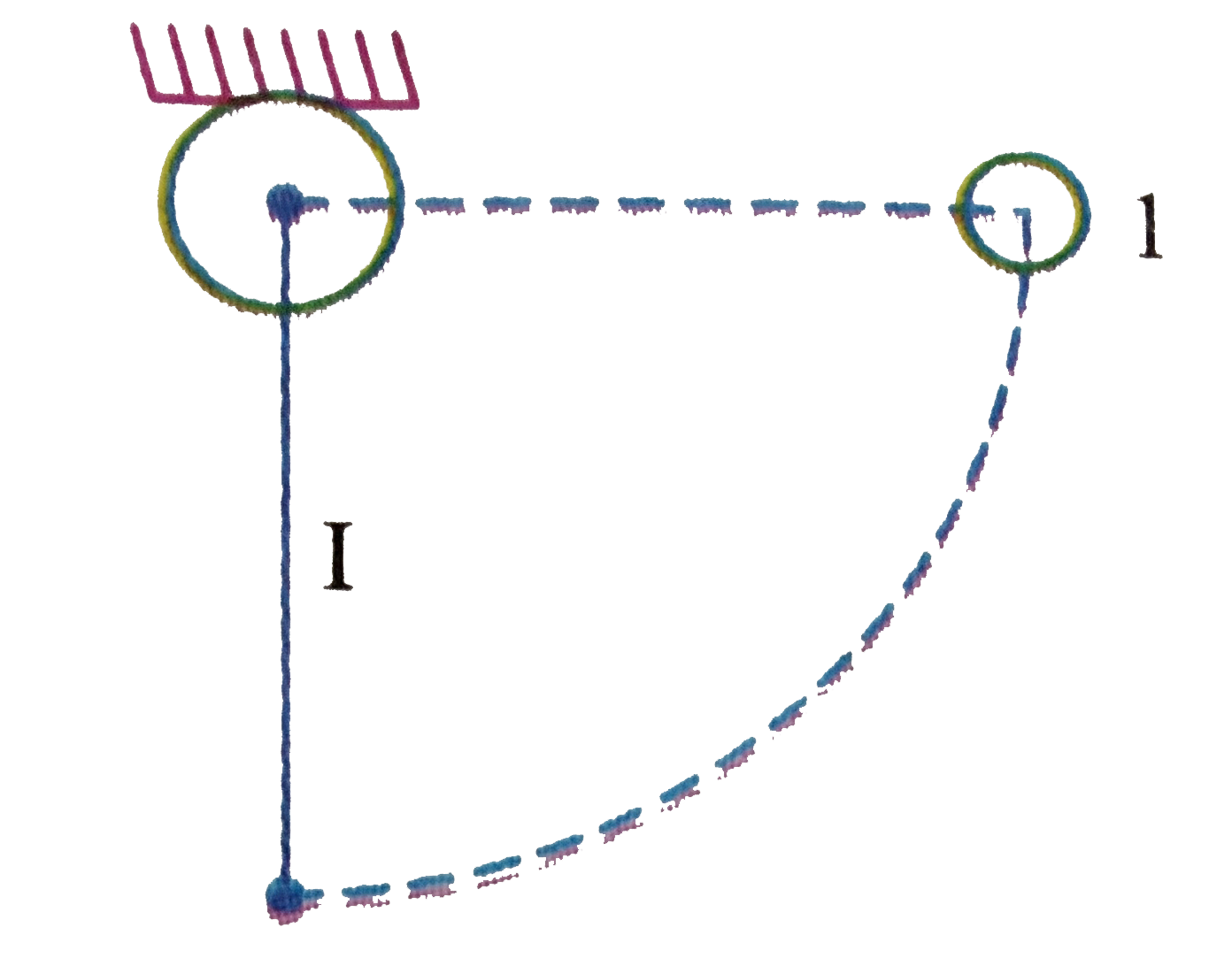
View SolutionA sphere of mass m attached with the free end of a steel wire of length l swings in the veritical plane form the horizontal positon.
Elongation of the wire in the vericle positon is
View SolutionA rod of mass m and length l is lying on a horizontal table. Work done in making it stand on one end will be
View Solution