Three equal charges, each having a magnitude of. 2.0×10−6C, are placed at the thre corners of a right. angled triangle of sides 3 cm, 4cm and 5 cm. find the three corner.
To solve the problem of finding the force on the charge at the right angle corner of a triangle formed by three equal charges, we can follow these steps:
Step 1: Identify the Charges and Their Positions
We have three equal charges, each of magnitude q=2.0×10−6C, placed at the corners of a right-angled triangle with sides 3 cm, 4 cm, and 5 cm. Let's denote the charges as follows:
- Charge q1 at point A (3 cm side)
- Charge q2 at point B (4 cm side)
- Charge q3 at point C (right angle corner)
Step 2: Calculate the Forces Acting on the Charge at the Right Angle Corner
We need to find the net force acting on the charge at point C due to the other two charges at points A and B.
Force due to Charge at A (F1):
- The distance between charges q1 and q3 is 3cm=0.03m.
- Using Coulomb's Law:
F1=k|q1⋅q3|r213
where k=9×109N m2/C2 and r13=0.03m.
Substituting the values:
F1=9×109⋅(2.0×10−6)2(0.03)2
F1=9×109⋅4.0×10−120.0009=9×109⋅4.4444×10−6=40N
Force due to Charge at B (F2):
- The distance between charges q2 and q3 is 4cm=0.04m.
- Using Coulomb's Law:
F2=k|q2⋅q3|r223
where r23=0.04m.
Substituting the values:
F2=9×109⋅(2.0×10−6)2(0.04)2
F2=9×109⋅4.0×10−120.0016=9×109⋅2.5×10−6=22.5N
Step 3: Calculate the Resultant Force
Since F1 and F2 act at right angles to each other, we can find the resultant force Fnet using the Pythagorean theorem:
Fnet=√F21+F22
Substituting the values:
Fnet=√(40)2+(22.5)2=√1600+506.25=√2106.25≈45.97N
Step 4: Determine the Direction of the Resultant Force
To find the angle θ that the resultant force makes with the horizontal (force from charge A), we can use:
tanθ=F2F1
Substituting the values:
tanθ=22.540=0.5625
Thus,
θ=tan−1(0.5625)≈29.74∘
Final Result
The net force acting on the charge at the right angle corner is approximately 45.97N at an angle of approximately 29.74∘ from the horizontal.
---
We have three equal charges, each of magnitude q=2.0×10−6C, placed at the corners of a right-angled triangle with sides 3 cm, 4 cm, and 5 cm. Let's denote the charges as follows:
- Charge q1 at point A (3 cm side)
- Charge q2 at point B (4 cm side)
- Charge q3 at point C (right angle corner)
We need to find the net force acting on the charge at point C due to the other two charges at points A and B.
- The distance between charges q1 and q3 is 3cm=0.03m.
- Using Coulomb's Law:
F1=k|q1⋅q3|r213
where k=9×109N m2/C2 and r13=0.03m.
Substituting the values:
F1=9×109⋅(2.0×10−6)2(0.03)2
F1=9×109⋅4.0×10−120.0009=9×109⋅4.4444×10−6=40N
- The distance between charges q2 and q3 is 4cm=0.04m.
- Using Coulomb's Law:
F2=k|q2⋅q3|r223
where r23=0.04m.
Substituting the values:
F2=9×109⋅(2.0×10−6)2(0.04)2
F2=9×109⋅4.0×10−120.0016=9×109⋅2.5×10−6=22.5N
Since F1 and F2 act at right angles to each other, we can find the resultant force Fnet using the Pythagorean theorem:
Fnet=√F21+F22
Substituting the values:
Fnet=√(40)2+(22.5)2=√1600+506.25=√2106.25≈45.97N
To find the angle θ that the resultant force makes with the horizontal (force from charge A), we can use:
tanθ=F2F1
Substituting the values:
tanθ=22.540=0.5625
Thus,
θ=tan−1(0.5625)≈29.74∘
The net force acting on the charge at the right angle corner is approximately 45.97N at an angle of approximately 29.74∘ from the horizontal.
Topper's Solved these Questions
- ELECTRIC FIELD AND POTENTIALBOOK - HC VERMACHAPTER - ELECTRIC FIELD AND POTENTIALEXERCISE - Short Answer
14 Videos
- ELECTRIC FIELD AND POTENTIALBOOK - HC VERMACHAPTER - ELECTRIC FIELD AND POTENTIALEXERCISE - Objective 1
9 Videos
- ELECTRIC FIELD AND POTENTIALBOOK - HC VERMACHAPTER - ELECTRIC FIELD AND POTENTIALEXERCISE - Exercises
75 Videos
- ELECTRIC CURRENT THROUGH GASESBOOK - HC VERMACHAPTER - ELECTRIC CURRENT THROUGH GASESEXERCISE - Exercises
23 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - HC VERMACHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - EXERCISE
9 Videos
Similar Questions
Three equal charges, each having a magnitude of 2×10−6C, are placed at the three corners of a right-angled triangle of sides 3, 4, and 5 cm. Find the force on the charge at the right-angled corner.
View SolutionThree identical charges, each having a value 1.0×10−8C, are placed at the corners of an equilateral triangle of side 20 cm find the electric field and potential at the centre of the triangle.
View Solution
Knowledge Check
The area of the circumcircle of a right angle triangle whose sides are 6 cm, 8 cm and 10 cm will be:
A9πcm2πB25πcm2C24.5πcm2D16πcm2Find the perimeter of a triangle with sides equal to 6 cm, 4 cm and 5 cm.
A14 cmB18 cmC20 cmD15 cmThe length of the three sides of a right angled triangle are (x−2)cm,xcmand(x+2)cmrespectively. Then the value of x is
A10B8C4D0
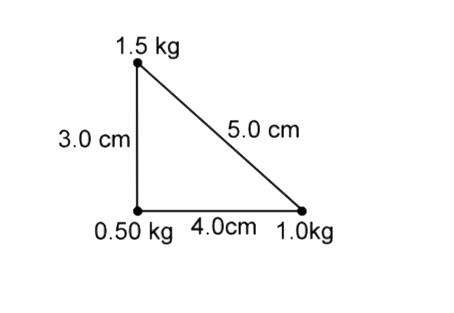
Three particles of masses 0.5 kg, 1.0 kg and 1.5 kg are placed at the three corners of a right angled triangle of sides 3.0 cm, 4.0 cm and 5.0 cm as shown in figure. Locate the centre of mass of the system.
View SolutionFind the greatest angle of the triangle whose sides measure 3 cm, 4 cm and 5 cm.
View SolutionThree point particles of masses 1.0 kg 2 kg and 3 kg are placed at three comers of a right angle triangle of sides 4.0 cm , 3.0 cm and 5.0 cm as shown in the figure . The centre of mass of the system is at point :

View SolutionCharge of 5μC each are placed at the corners of an equilateral triangle of side 10 cm. Then the force on each charge is :-
View SolutionThree equal masses each of 50 g, are placed at the corners of a right angled isoceles triangle whose two equal sides are 5 cm each. The position of the centre of mass of the system is
View Solution
