Question

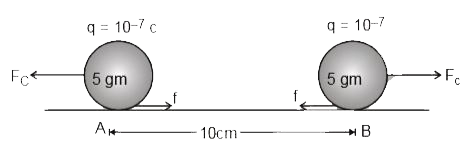
Two particles, each having a mass of 5 g and charge. $1.0\times {10}^{-7}$ C, stay in limiting wquilibrium on a horizontal. table with a seaprtion of 10 cm between them. The coefficient of friction beteen each partcle and the table. is the same. Find the value of this coefficient.

Explanation

To solve the problem step by step, we will follow these instructions:

Step 1: Identify the Given Data
- Mass of each particle, \( m = 5 \, \text{g} = 5 \times 10^{-3} \, \text{kg} \)
- Charge of each particle, \( q = 1.0 \times 10^{-7} \, \text{C} \)
- Separation between the particles, \( r = 10 \, \text{cm} = 0.1 \, \text{m} \)

Step 2: Calculate the Gravitational Force (Normal Force)
The normal force \( N \) acting on each particle is equal to its weight:
\( N = mg = (5 \times 10^{-3} \, \text{kg}) \times (9.8 \, \text{m/s}^2) = 0.049 \, \text{N} \)

Step 3: Calculate the Coulomb Force
The Coulomb force \( F_c \) between the two charges can be calculated using Coulomb's law:
\( F_c = k \frac{q_1 q_2}{r^2} \)
Where \( k = 9 \times 10^9 \, \text{N m}^2/\text{C}^2 \).

Substituting the values:
\( F_c = 9 \times 10^9 \frac{(1.0 \times 10^{-7})^2}{(0.1)^2} \)
\( F_c = 9 \times 10^9 \frac{1.0 \times 10^{-14}}{0.01} = 9 \times 10^9 \times 1.0 \times 10^{-12} = 0.009 \, \text{N} \)

Step 4: Relate the Frictional Force to the Coulomb Force
In limiting equilibrium, the frictional force \( f \) is equal to the Coulomb force:
\( f = F_c \)
The frictional force can also be expressed as:
\( f = \mu N \)
Where \( \mu \) is the coefficient of friction.

Step 5: Set Up the Equation
Equating the two expressions for the frictional force:
\( \mu N = F_c \)
Substituting the values:
\( \mu (0.049) = 0.009 \)

Step 6: Solve for the Coefficient of Friction \( \mu \)
Rearranging the equation to solve for \( \mu \):
\( \mu = \frac{0.009}{0.049} \approx 0.1837 \)

Final Answer
The coefficient of friction \( \mu \) is approximately \( 0.18 \).

---