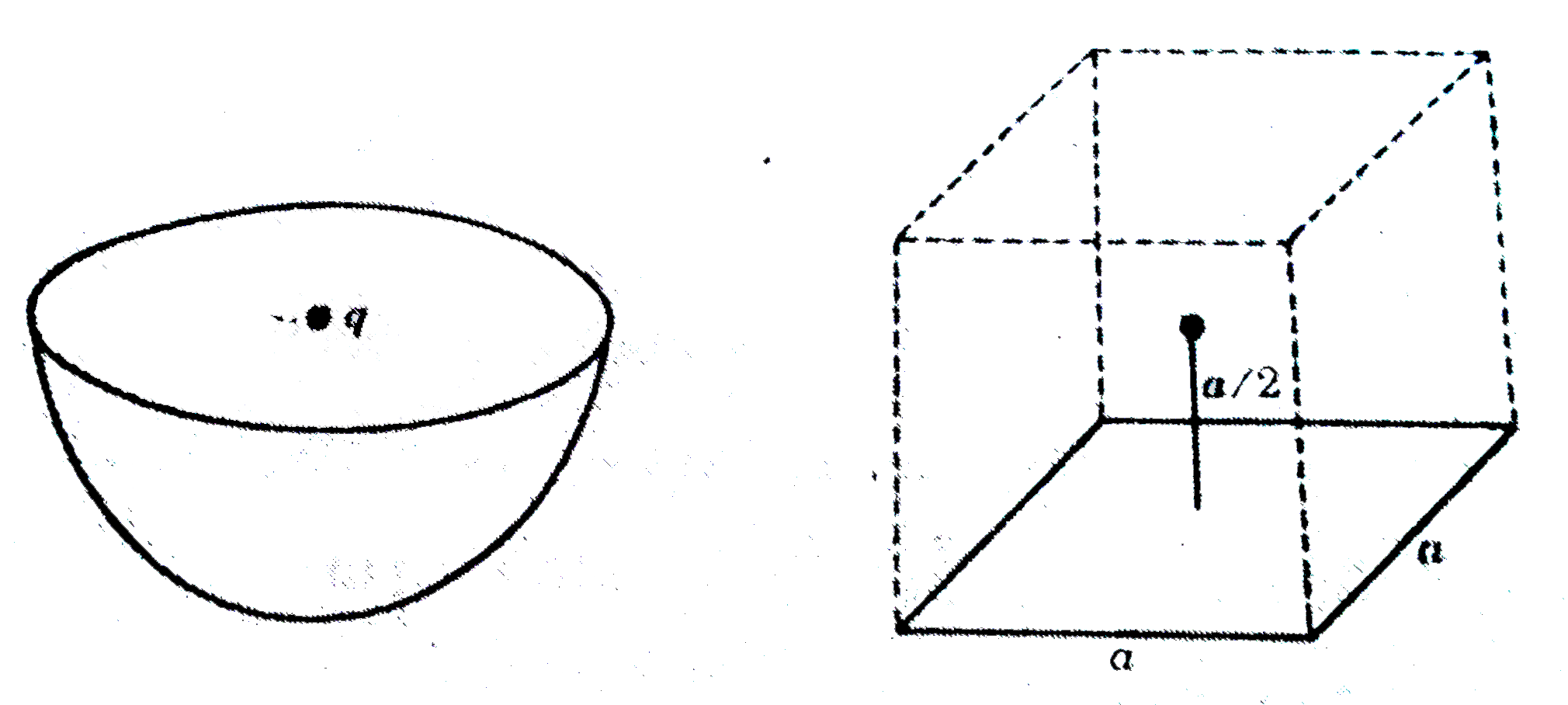A charge Q is placed at a distance α2 above the centre of a horizontal, spuare surface of edge a as shown in figure (30-E1). Find the flux of the electric field through the square surface.
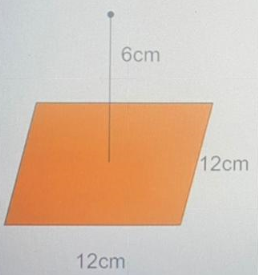
Given ,a charge is placed on a plane
surface with area= a2
About a/2 form it's centre
Assumption : Let us assume that the
given plane forms a surface of imaginary
cube than the charge is found to be at the
centre of the cube.
Hence flux through the surface
=(Qε0)×16=(Q6(ε0)) .
Topper's Solved these Questions
Similar Questions
Knowledge Check
A point charge 'q' is placed at a distance l' (on th y-axis) vertically above the surface which lies in the xz plane as shown in the figure. The flux of electric field passing through the plate is
 Aq6ε0Bq18ε0C124ε0Dq48ε0
Aq6ε0Bq18ε0C124ε0Dq48ε0The flux of electric field due to these charges through the surface S is
 A2qε0B3qε0C−5qε0Dqε0
A2qε0B3qε0C−5qε0Dqε0A charge q is placed at the centre of the cubical vessel (with one face a open) as shown in figure. The flux of the electric field through the complete vessel is
 Aq/6ε0Bq/ε0C5q/6ε0Dq/4ε0
Aq/6ε0Bq/ε0C5q/6ε0Dq/4ε0
A charge Q is placed at the centre of a cub. Find the flux of the electric field through the six surfaced of the cube.
View Solution(a) Define electric flux. Is is the scalar or a vector quantity?
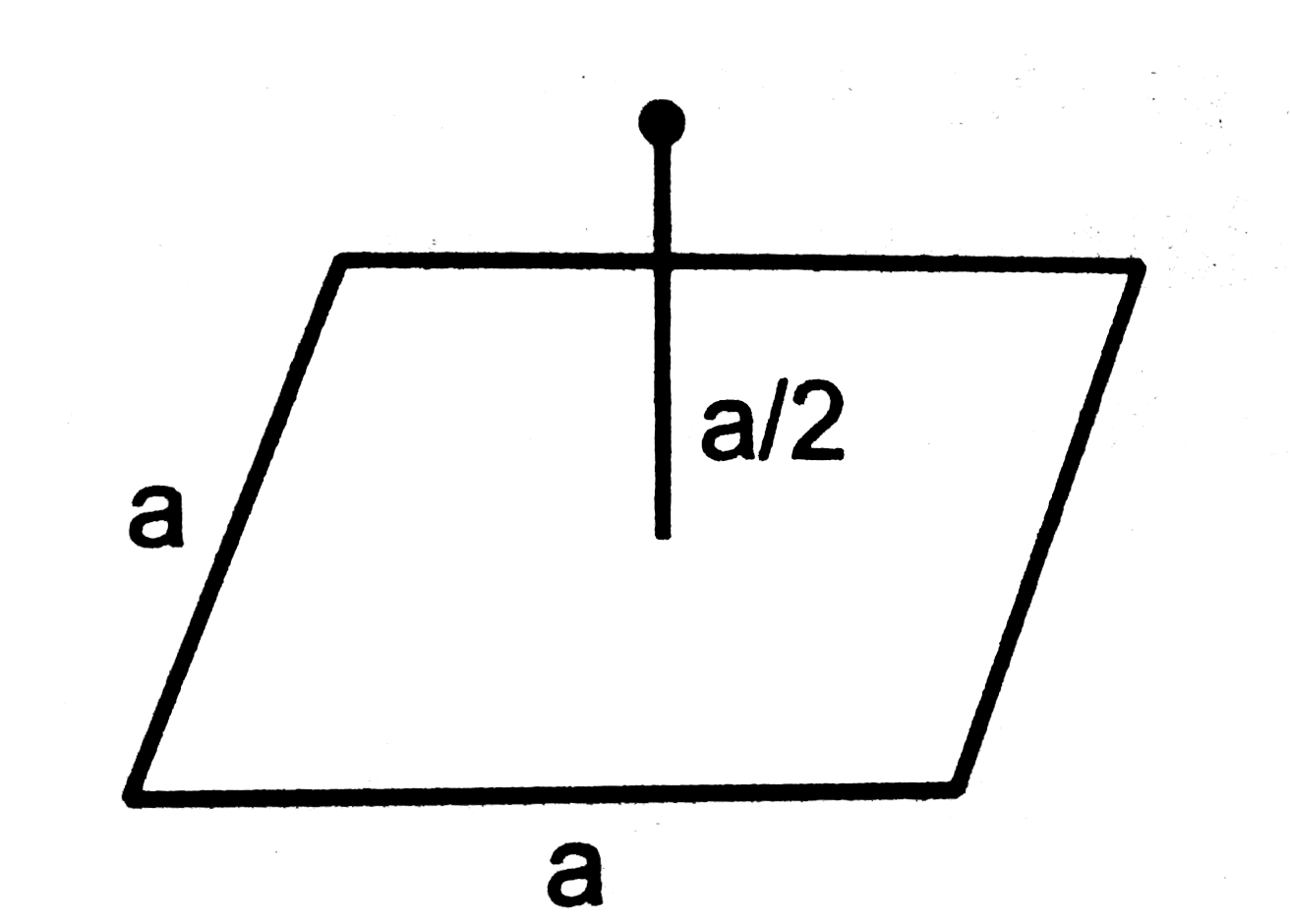
A point charge q is at a distance of d/2 directly above the centre of a square of side d, as shown in the figure. Use Gauss's law to obtain the expression for the electric flux through the square.
(b) If the point charges is now moved to a distance 'd' from the centre of the square and the side of the square is doubled, explain how the electric flux will be affected.

View SolutionA point charge of +12μC is at a distance 6 cm vertically above the centre of a square of side 12 cm as shown in figure. The magnitude of the electric flux through the square will be _______ ×103Nm2/C.
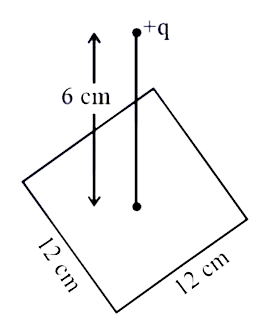
View SolutionA point charge +20muC is at a distance 6 cm directly above the centre of a square of side 12 cm as shown is figure. The magnitude of electric flux through the square is
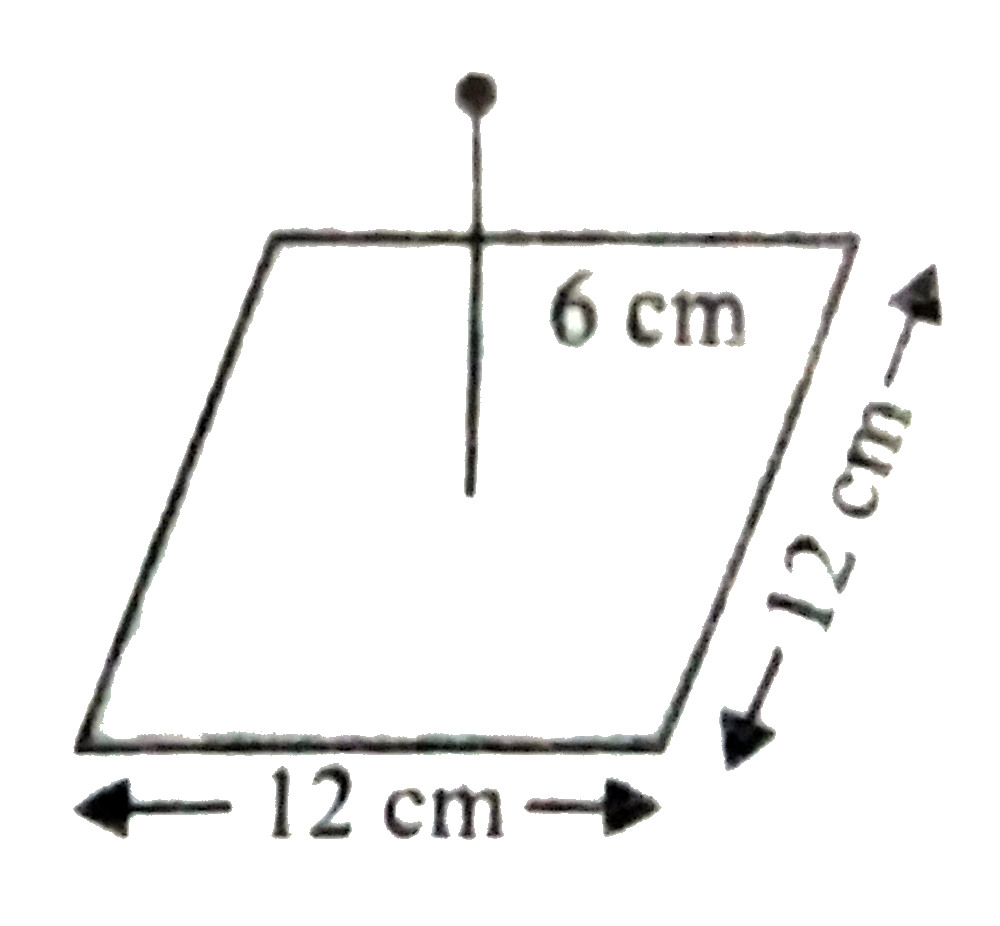
View SolutionA point charge q is placed at a distance a/2 directly above the center of a square of side a. The electric flux through the square is
View Solution