One end of a 10 cm long silk thread is fixed to a large vertical surface of a xharged nonconducting plate and the other end is fastened to a small ball having a mass of 10 g and charge of 4.0×10C. In equilibrium, the thread make an angle of 600 with the vertical. Find the surface charge dendity on the plate.
T cos60∘ = mg
Tsin60∘=qE
tan60∘=qEmg
E=(mgtan60∘q)=σ2ε0
So,σ=(2ε0mgtan60∘q)
=(2×8.8×(10−12)×10×(10−3)×9.8×1.7324.0×(10−6))
=7.5×(10−7)cm2 .
Topper's Solved these Questions
Similar Questions
The particle P shown has amass of 10mg and a charge of−0.01μC.Each plate has a surface area
View SolutionA particle of mass m and charge q is suspended from a point A with a silk thread of length l. Another particle of charge −q is fixes at a distance I from the point A such that point A and the charge -q lie in same horizontal plane. If at equilibrium , the thread makes angle 30∘ with vertical, find the mass m and tension in the thread . ( Take acceleration due to gravity as g).
View Solution
Knowledge Check
If a small sphere of mass m and charge q is hung from a silk thread at an angle θ with the surface of a vertical charged conducting plate, then for equilibrium of sphere, the surface charge density of the plate is
Aε0(mgq)tanθBε0(2mgq)tanθCε0(mgq)tanθDε0(mg3q)tanθIf a small sphere of mass m and charge q is hanged from a silk thread at an angle θ with the surface of a vectical charged conductinb plate, then for equilibrium of sphere the surface charge density of the plate -
Aε0mgtanθqB(2ε0mgtanθ)/qCε0mgqtanθDε0mgtanθ3qTwo identical tennis balls each having mass 'm' and charge 'q' are suspended from a fixed point by threads of length 'l'. What is the equilibrium separation when each thread makes a small angle 'θ' with the vertical ?
Ax=(q2l2πε0mg)1/2Bx=(q2l2πε0mg)1/3Cx=(q2l22πε0m2g)1/3Dx=(q2l22πε0m2g2)1/3
Three identical small balls, each of mass 0.1 g, are suspended at one point on silk thread having a length of l=20cm . What charges should be imparted to the balls for each thread to form an angle of α=30∘ with the vertical?
View SolutionA rod of length 1.0m and mass 0.5kg fixed at ond is initially hanging vertical. The other end is now raised until it makes an angle 60∘ with the vertical. How much work is required?
View SolutionThere is one large vertical non-conducting plane surface with uniformly distributed charge. A pendulum bob is suspended through an insulating string from a point on this non-conducting surface. The length of the string is l and mass of the bob is m. The charge carried by the pendulum bob is q. It is found that in a state of equilibrium, the string of the pendulum makes 60∘ angle with the vertical. What will be the charge per unit area on surface? Also calculate the tension developed in the string in equilibrium state.
View SolutionAn electric dipole consists of charges ±2.0×10−8 C separated by distance of ±2.0×10−3m. It is placed at a distance of 6 cm from a line charge of linear charge density 4.0×10−4Cm−1 as shown in figure such that the dipole makes an angle of θ=60∘ with line AB. Find the force acting on the dipole.

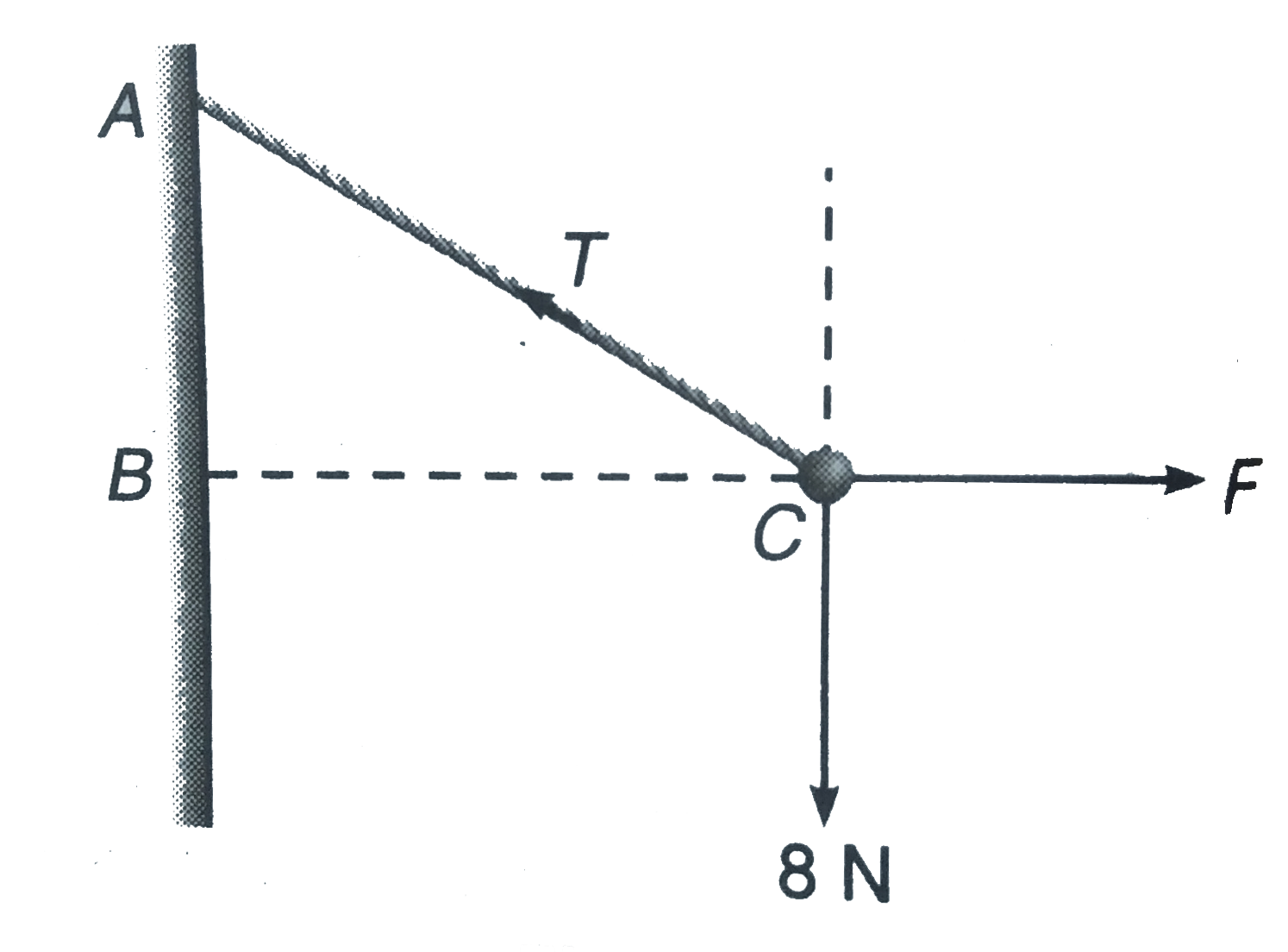
View SolutionOne end of a string 0.5m long is fixed to a point A and the other end is fastened to a small object of weight 8N. The object is pulled aside by a horizontal force F, until it is0.3m from the vertical through A. Find the magnitudes of the tension T in the string and force F.
View Solution
