Find the energy stored in a capacitor of capacitance 100μF when it is charged to a potential difference of 20 V.
0.02J
0.04J
0.01J
0.05J
The correct Answer is:A
To find the energy stored in a capacitor, we can use the formula:
U=12CV2
where:
- U is the energy stored in the capacitor,
- C is the capacitance of the capacitor,
- V is the potential difference across the capacitor.
Step 1: Identify the given values
- Capacitance C=100μF=100×10−6F
- Potential difference V=20V
Step 2: Substitute the values into the formula
Now we can substitute the values of C and V into the energy formula:
U=12(100×10−6F)(20V)2
Step 3: Calculate V2
First, calculate V2:
V2=(20V)2=400V2
Step 4: Substitute V2 back into the equation
Now substitute V2 back into the equation for U:
U=12(100×10−6)(400)
Step 5: Calculate U
Now perform the multiplication:
U=12(100×400×10−6)=12(40000×10−6)=20000×10−6J
Step 6: Convert to Joules
Finally, convert 20000×10−6J to standard form:
U=0.02J
Final Answer
The energy stored in the capacitor is:
U=0.02J
---
- U is the energy stored in the capacitor,
- C is the capacitance of the capacitor,
- V is the potential difference across the capacitor.
- Capacitance C=100μF=100×10−6F
- Potential difference V=20V
Now we can substitute the values of C and V into the energy formula:
First, calculate V2:
Now substitute V2 back into the equation for U:
Now perform the multiplication:
Finally, convert 20000×10−6J to standard form:
The energy stored in the capacitor is:
Topper's Solved these Questions
- CAPACITORSBOOK - HC VERMACHAPTER - CAPACITORSEXERCISE - Worked Out Examples
23 Videos
- CAPACITORSBOOK - HC VERMACHAPTER - CAPACITORSEXERCISE - Short Answer
7 Videos
- BOHR'S MODEL AND PHYSICS OF THE ATOMBOOK - HC VERMACHAPTER - BOHR'S MODEL AND PHYSICS OF THE ATOMEXERCISE - Exercises
46 Videos
- DISPERSION AND SPECTRABOOK - HC VERMACHAPTER - DISPERSION AND SPECTRAEXERCISE - Exercises
11 Videos
Similar Questions
Obtain the expression for the energy stored in a parallel plate capacitor of capacitance C charged to a potential V.
View SolutionA capacitor of capacitance 5 μF is charged to a potential difference of 10 volts and another capacitor of capacitance 9 μF is charged to a potential difference of 8 volts. Now these two capacitors are connected in such a manner that the positive plate of one is connected to the positive plate of other. Calculate the common potential difference across the two capacitors.
View Solution
Knowledge Check
The charge and energy stored in the capacitor of capacity 32μF, when it is charged to a potential difference of 0.6 kV are respectively
A1.92×10−2C,5.76JB2.92×10−2C,5.76JC1.92×102C,5.76JD1.92×10−2C,4.76JThe energy stored in a capacitor of capacitance 100μF is 50 J. Its potential difference is
A50 VB500 vC1000 VD1500 VA capacitor of capacitance 50μF is charged to 10 V. Its electrostatic potential energy is
A2.5×10−3JB2.5×10−4JC5×10−2JD1.2×10−5J
A capacitor of capacitance C1 is charged to a potential V1 , while another capacitor of capacitance C2 is charged to a potential difference V2 . The capacitors are now disconnected from their respective charging batteries and connected in parallel to each other
Find the total energy stored in the two capacitors before they are connected .
View SolutionA capacitor of capacitance C1 is charged to a potential V1 , while another capacitor of capacitance C2 is charged to a potential difference V2 . The capacitors are now disconnected from their respective charging batteries and connected in parallel to each other
Find the total energy stored in the parallel combination of two capacitors.
View SolutionA capacitor of capacitance C1 is charged to a potential V1 while another capacitor of capacitance C2 is charged to a potential difference V2 . The capacitors are now disconnected from their respective charging batteries and connected in parallel to each other .
(a) Find the total energy stored in the two capacitors before they are connected.
(b) Find the total energy stored in the parallel combination of the two capacitors.
(c ) Explain the reason for the difference of energy in parallel combination in comparison to the total energy before they are connected.
View SolutionA capacitor of capacitance 50μF is charged to 100 volts. Its energy is equal to
View SolutionCalculate the energy stored in the capacitor of capacitance 2μf. The voltmeter gives a reading of 15 V and the ammeter A reads 15mA .
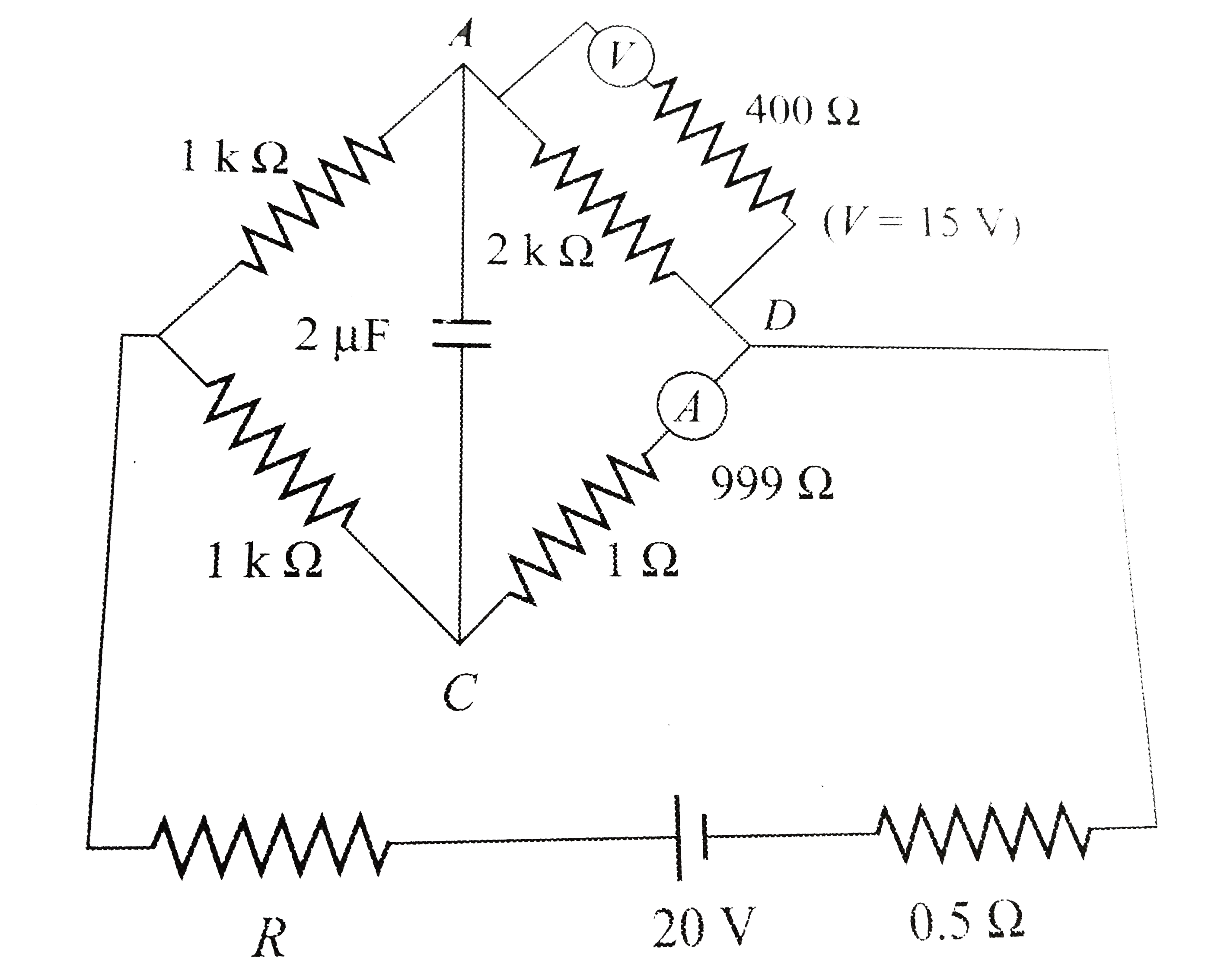
View Solution
