The bohrradius is given by a0=ε0h2πme2 verify that the KHS has dimesions of length
The correct Answer is:A
a=∈0h2πme2=A2T2(ML2T−1)M2L3T−2=L
=M2L2T−2M2L3T−2=L
Clearly a0 has dimensions of length.
Topper's Solved these Questions
Similar Questions
The dimensions of 1ε0e2hc are
View SolutionHydrogen Atom and Hydrogen Molecule
The observed wavelengths in the line spectrum of hydrogen atom were first expressed in terms of a series by johann Jakob Balmer, a Swiss teacher. Balmer's empirical empirical formula is
1λ=RH(122−1n2), N=3,4,5
RH=Mee48ε20h3c=109.678cm−1
Here,
RH is the Rydberg Constant, me is the mass of electron. Niels Bohr derived this expression theoretically in 1913. The formula is easily generalized to any one electron atom//ion.
Determine the loest energy and the radius of the Bohr orbit of the muonic hydrogen atom. Ignore the motion of the nucleus in your calculation. The radius of the Bohr orbit of a hydrogen atom
(called the Bohr radius,a0=ε0h2mee2∏is0.53Å)
The classical picture of an ''orbit'' in Bohr's theory has now been replaced by the quantum mechanical nation of an 'orbital'. The orbital ψ1σ1s(r) for the ground state of a hydrogen atom is given by
ψ1s(r)=1√∏a30era0
where r is the distance of the electron from the nucleus and a0 is the Bohr radius.
View Solution
Knowledge Check
The dimesions of (μ0ε0)−1/2 are
A[L−1T]B[LT−1]C[L−1/2T1/2]D[L1/2T−1/2]The dimensions of (μ0ε0)−1/2 are
A[L1/2T−1/2]B[L−1T]C[LT−1]D[L1/2T1/2]A quantity X is given by me48ε20ch3 where m is the mass of electron, e is the charge of electron, ε0 is the permittivity of free space, c is the velocity of light and h is the Planck's constant. The dimensional formula for X is the same as that of
AlengthBfrequencyCvelocityDwave number
Find the dimension of 1(4π)ε0e2hc)
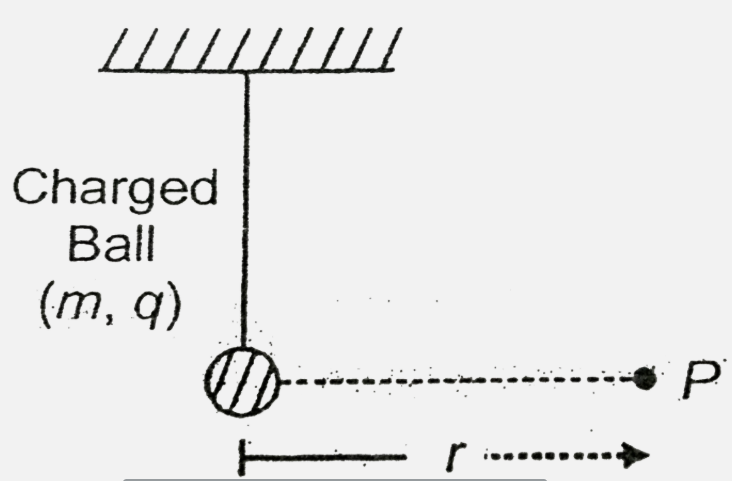
View SolutionThe electric field at point P due to a charged ball is given by
Ep=14πε0qr2
To measure 'E' at point P, A test charge q0 is placed at point P and measure electric force F upon the test charge. Check whether Fq0 is equal to 14πε0qr2 or not .
View SolutionFind the dimension of the quantity 14πε0e2hc, the letters have their usual meaning , ε0 is the permitivity of free space, h, the Planck's constant and c, the velocity of light in free space.
View SolutionIn the Bohr model of a π−mesic atom , a π−mesic of mass mπ and of the same charge as the electron is in a circular orbit of ratio of radius r about the nucleus with an orbital angular momentum h/2π. If the radius of a nucleus of atomic number Z is given by R=1.6×10−15Z13m, then the limit on Z for which (ε0h2/πme2=0.53Åandmπ/me=264)π−mesic atoms might exist is
View SolutionIf e is the electronic charge, c is the speed of light in free space and h is Planck's constant, the quantity 14πε0|e|2hc has dimensions of :
View Solution
