A parallel plate capacitor has plate area A and plate separation d. The space between the plates is filled up to a thickness x<d with a dielectric constant K. Calculate the capacitance of the system.

2KεAKd−x(K−1)
KεAK2d−x(K−1)
KεAK−x(K−1)
KεAKd−x(K−1)
The correct Answer is:D
The situation is shown in . The given system is equivalent to the series combinaton of two capacitors, one between a and c and the other between c and b. Here c represents the upper surface of the dielectric. This is because the potential at the upper surface of the dielectric is constant and we can imagine a thin metal plate being placed there. The capacitance of the capacitor between a and c is <br>C_1 = (Kepsilon_o A)/(x)<br> and the between c and b is <br>C_2 = (epsilon_0A)/(d-x)<br>. The equivalent capacitance is <br>C=(C_1C_2)/(C_1 +C_2) = (Kepsilion_A)/(Kd - x(K-1)<br>.
Topper's Solved these Questions
- CAPACITORSBOOK - HC VERMACHAPTER - CAPACITORSEXERCISE - Worked Out Examples
23 Videos
- CAPACITORSBOOK - HC VERMACHAPTER - CAPACITORSEXERCISE - Short Answer
7 Videos
- BOHR'S MODEL AND PHYSICS OF THE ATOMBOOK - HC VERMACHAPTER - BOHR'S MODEL AND PHYSICS OF THE ATOMEXERCISE - Exercises
46 Videos
- DISPERSION AND SPECTRABOOK - HC VERMACHAPTER - DISPERSION AND SPECTRAEXERCISE - Exercises
11 Videos
Similar Questions
The capacitance of a parallel plate capacitor with plate area A and separation d is C. The space between the plates in filled with two wedges of dielectric constants K1 and K2 respectively. Find the capacitance of resulting capacitor.

View SolutionThe capacitance of a parallel plate capacitor with plate area A and separation d is C. The space between the plates in filled with two wedges of dielectric constants K1 and K2 respectively. Find the capacitance of resulting capacitor.

View Solution
Knowledge Check
A parallel plate capacitor has plate area A and plate separation d. The space between the plates is filled up to a thickness x<d with a dielectric constant K. Calculate the capacitance of the system.
 A2KεAKd−x(K−1)BKεAK2d−x(K−1)CKεAK−x(K−1)DKεAKd−x(K−1)
A2KεAKd−x(K−1)BKεAK2d−x(K−1)CKεAK−x(K−1)DKεAKd−x(K−1)In a parallel-plate capacitor of plate area A, plate separation d and charge Q the force of attraction between the plates is F.
AF∝Q2BF∝1ACF∝dDF∝1dA parallel plate capacitor of plate area A and separation d is filled with two materials each of thickness d2 and dielectric constants ∈1 and ∈2 respectively. The equivalent capacitance will be
 A∈0Ad(∈1+∈2)B∈0Ad(∈1+∈2)∈1∈2C2∈0Ad∈1∈2(∈1+∈2)D2∈0Ad(∈1+∈2)∈1∈2
A∈0Ad(∈1+∈2)B∈0Ad(∈1+∈2)∈1∈2C2∈0Ad∈1∈2(∈1+∈2)D2∈0Ad(∈1+∈2)∈1∈2
Figure shown a parallel-plate capacitor having square plates of edge a and plate-separation d. The gap between the plates is filled with a dielectric of dielectric constant K which varies parallel to an edge as K=K0+αx, where K and α are constants and x is the distance from the left end. Calculate the capacitance.

View SolutionA parallel plate capacitor with plate area A & plate separation d is filled with a dielectric material of dielectric constant given byK=K0(1+αx).. Calculate capacitance of system: (given αd<<1).

View SolutionFig shows a parallel plate capacitor of plate area A and plate separation d. Its entire space is filled with three different dielectric slabs of same thickness. Find the equivalent capacitance of the arrangment.
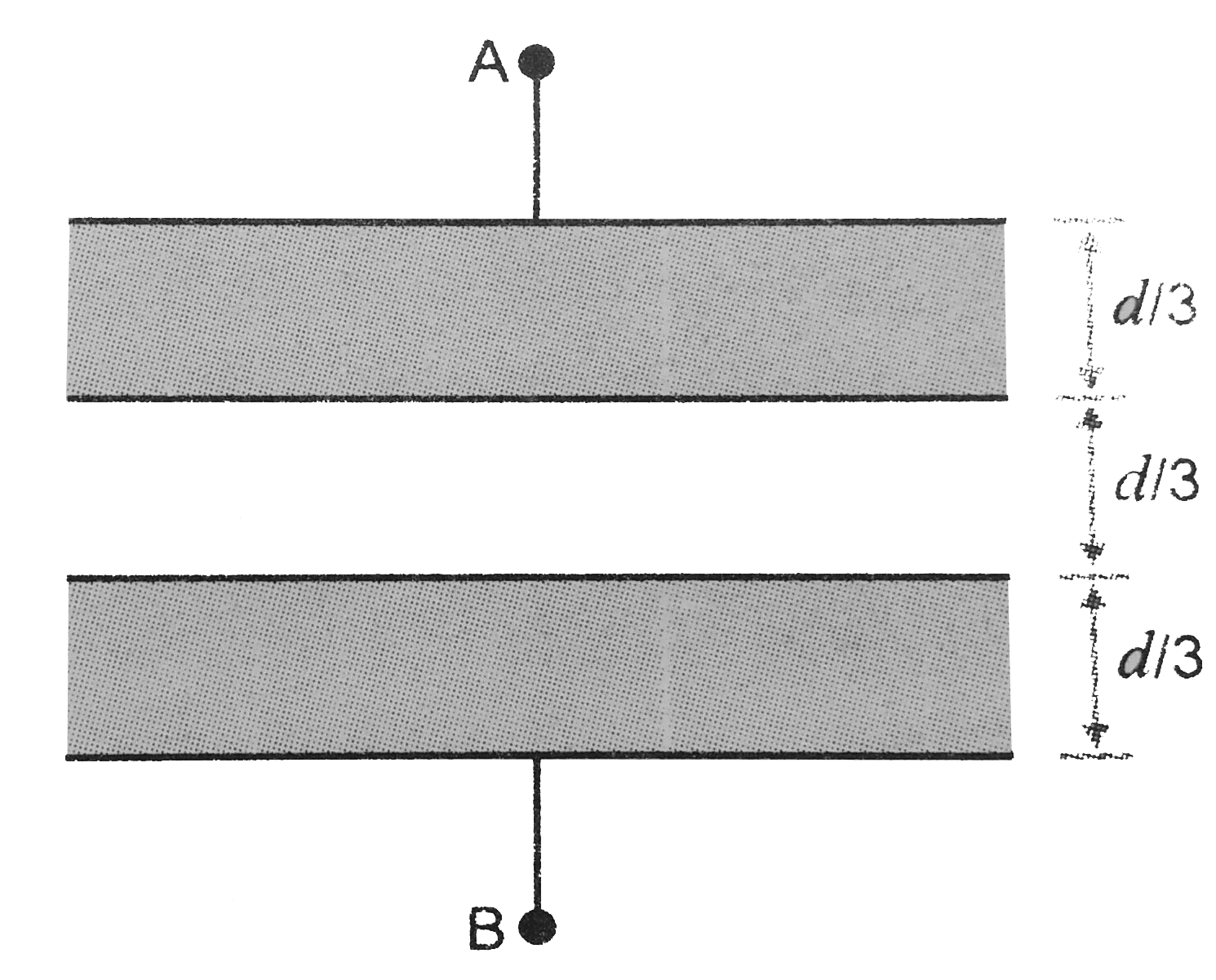
View SolutionA parallel plate capacitor having plate area A and separation between the plates d is charged to potential V.The energy stored in capacitor is ....???
View SolutionA parallel plate air capacitor has capacitance C. Half of space between the plates is filled with dielectric of dielectric constant K as shown in figure . The new capacitance is C . Then

View Solution