A finite ladder is constructed by connecting several sections of capacitor combinations as shown in figure . It is terminated by a capacitor of capacitance C . What value should be chosen for C, such that the equivalent capacitance of the number of sections in between ?
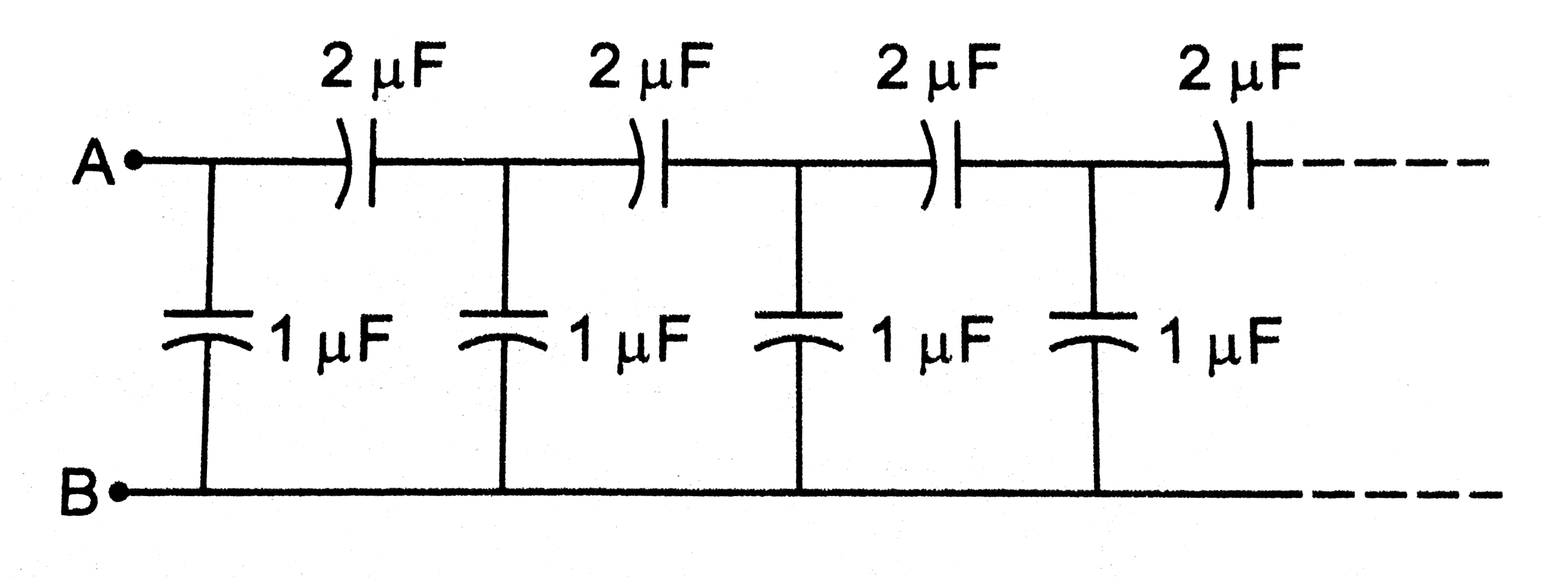
AB = C and are in series So are imparallel
Then and are
(impossible )
So,
The value of C is
Topper's Solved these Questions
- CAPACITORSBook:HC VERMAChapter:CAPACITORSExercise:Exercise
Explore 2 Videos
- CAPACITORSBook:HC VERMAChapter:CAPACITORSExercise:Objective 2
Explore 7 Videos
- BOHR'S MODEL AND PHYSICS OF THE ATOMBook:HC VERMAChapter:BOHR'S MODEL AND PHYSICS OF THE ATOMExercise:Exercises
Explore 46 Videos
- DISPERSION AND SPECTRABook:HC VERMAChapter:DISPERSION AND SPECTRAExercise:Exercises
Explore 11 Videos
Similar Questions
A finite ladder circuit is constructed by connecting several sections of 6μF,8μF capacitor combinations as shown in the figure. Circuit is terminated by a capacitor of capacitance C. Find the value of C, such that the equivalent capacitance of the ladder between the points A and B becomes independent of the number of sections in between ?

View SolutionSome capacitors each of capacitance 30μF are connected as shown in. Calculate the equivalent capacitance between terminals A and B
 .
.
View Solution
Knowledge Check
An infinite ladder is constructed by connecting several sections of 2 μF,4μF capacitor combination as shown in figure . It is terminated by a capacitor of capacitance C. What value should be chosen for C such that the equivalent capacitance of the ladder between points A and B becomes independent of the number of sections in between
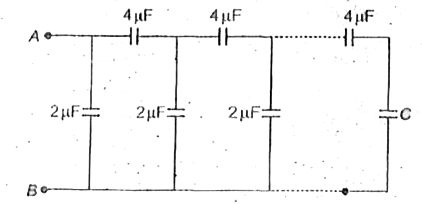 A18μ FB6μ FC2μ FD4μ F
A18μ FB6μ FC2μ FD4μ FA finite ladder is constructed by connecting several sections of 3μF,6μF capacitor combination as shown. The value of C such that the equivalent capacitance of ladder between the points A and B becomes independent of the number of section in between
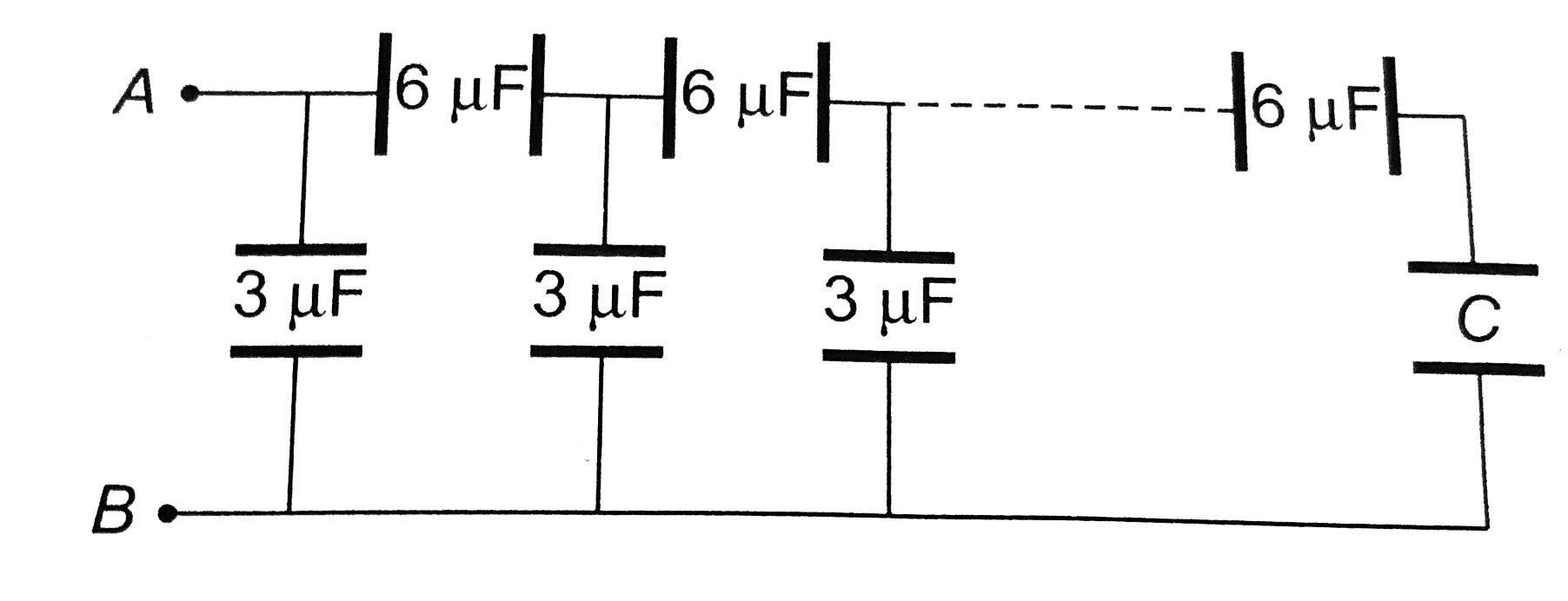 A2μFB4μFC6μFD8μF
A2μFB4μFC6μFD8μFIn the circuit shown in figure, the charge stored on a capacitor of capacitance 3μF is
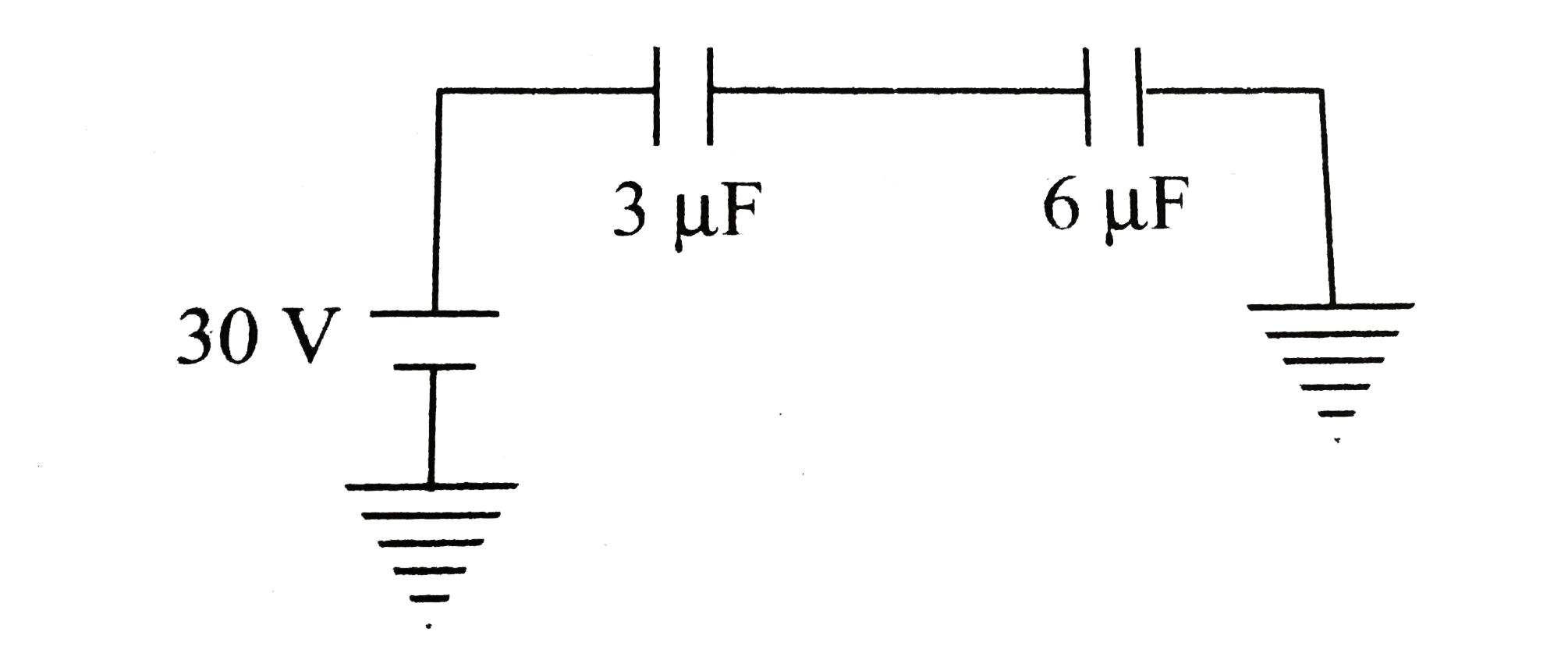 AzeroB40μCC60μCD90μC
AzeroB40μCC60μCD90μC
Five capacitors each of capacitance 20μF are joined as shown in the figure. The equivalent capacitance between A and C is

View Solution
Calculate the capacitance of the capacitor in figure. If the equivalent capacitance of the combination between A and B is 15μF.
View SolutionFour capacitors, each of capacitance 4μF, are connected as shown here. The equivalent capacitance between the points A and B will be
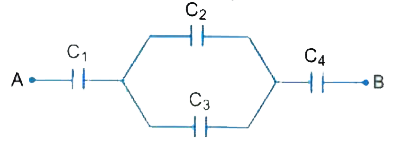
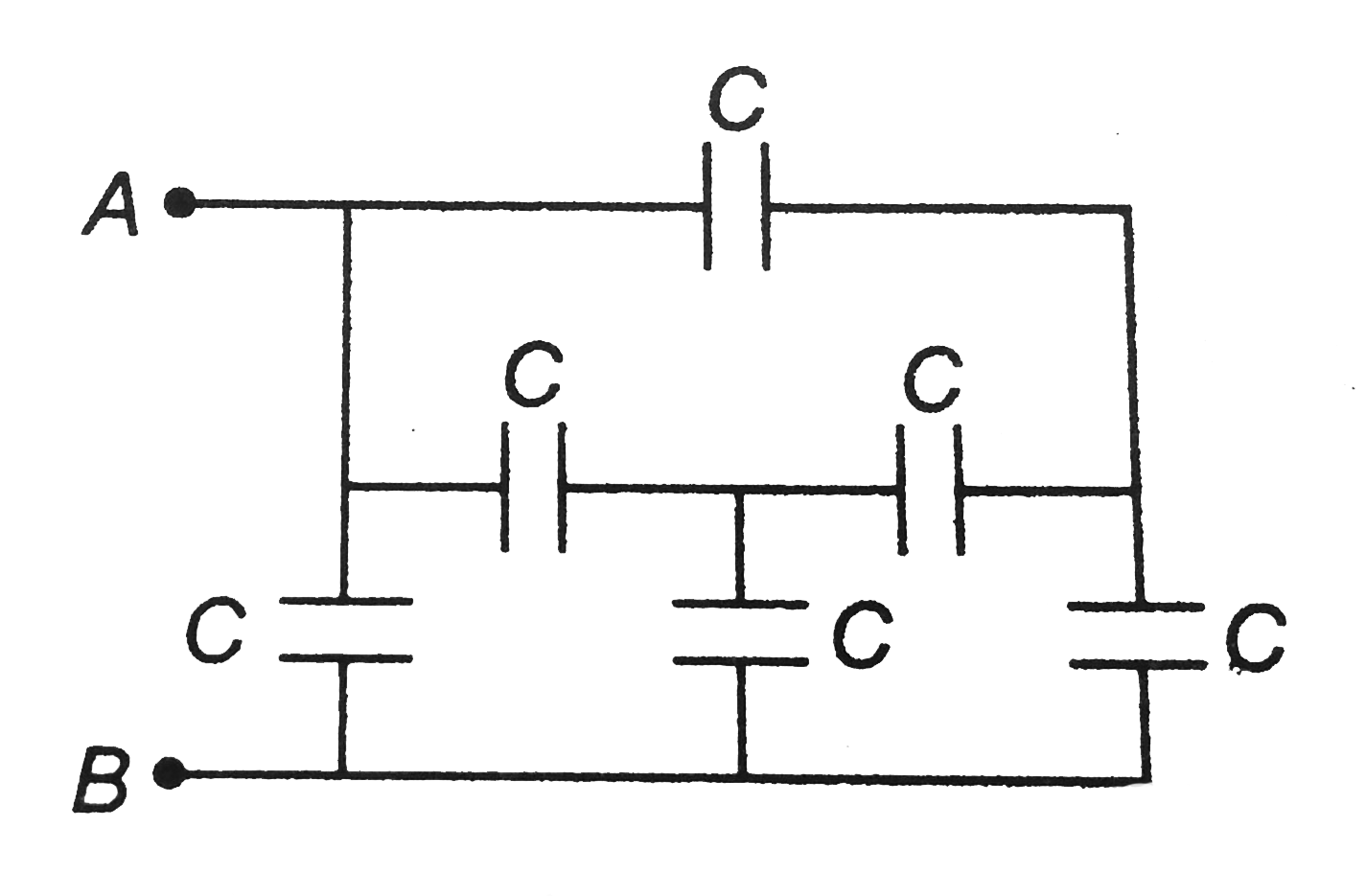
View SolutionSix equal capacitors each of capacitance C are connected as shown in the figure. The equivalent capacitance between points A and B is
View SolutionThree equal capacitors, each with capacitance C are connected as shown in figure. Then the equivalent capacitance between A and B is
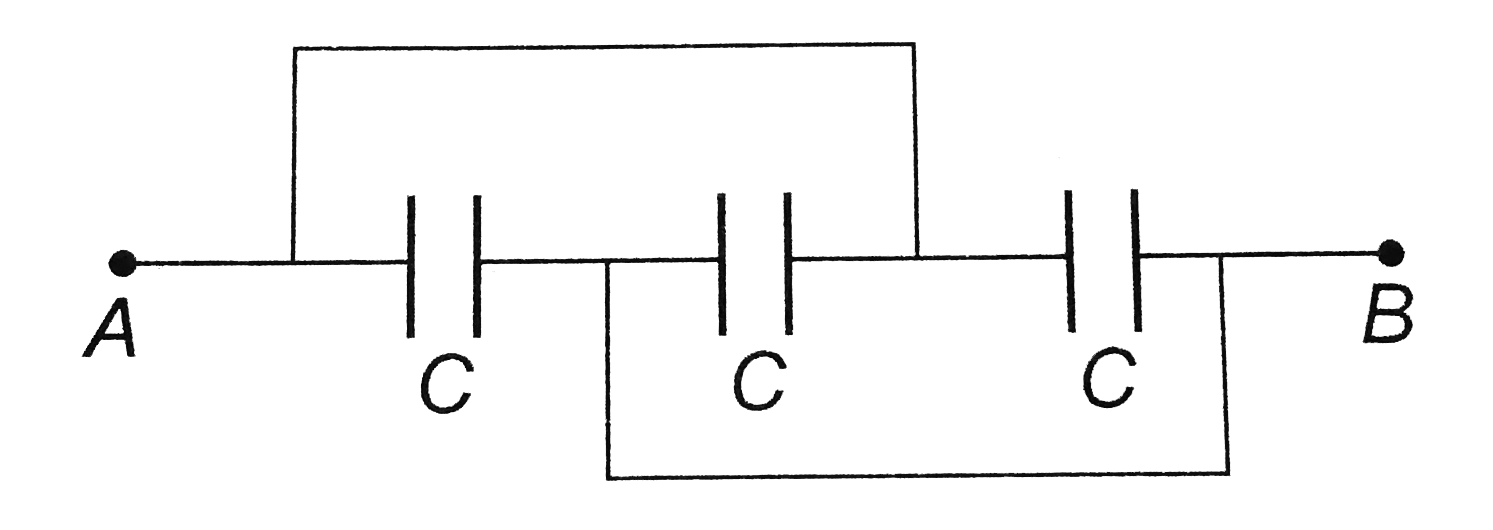
View Solution