A capacitor of capacitance 100(μ)F is charged by connecting it to a battery of emf 12 V and internal resistance 2(Ω). (a) Find the time constant of the circuit. (b) Find the time taken before 99% of maximum charge is stored on the capacitor.
The time constant is ltbr>(τ)=CR=(100(τ)F)(2(Ω)=200(τ)s.
the charge at time t is
q=(ε)C(1−e−tCR).
Putting q=0.99(ε)C,
0.99=1−e−t(200(μ)s)<br>,-(t)/(200(mu))=1n(0.01)<br>or, t=920(mu)s=0.92ms.
Topper's Solved these Questions
- ELECTRIC CURRENT IN CONDUCTORSBOOK - HC VERMACHAPTER - ELECTRIC CURRENT IN CONDUCTORSEXERCISE - Worked Out Examples
32 Videos
- ELECTRIC CURRENT IN CONDUCTORSBOOK - HC VERMACHAPTER - ELECTRIC CURRENT IN CONDUCTORSEXERCISE - worked out Example
1 Videos
- DISPERSION AND SPECTRABOOK - HC VERMACHAPTER - DISPERSION AND SPECTRAEXERCISE - Exercises
11 Videos
- ELECTRIC CURRENT THROUGH GASESBOOK - HC VERMACHAPTER - ELECTRIC CURRENT THROUGH GASESEXERCISE - Exercises
23 Videos
Similar Questions
A capacitor of capacitance 100(μ)Fisco∩ectedacrossabaeryofemf6.0Vthrougharesistanceof20k(Omega)for 4.0s after the battery is disconnecting?
View SolutionA capacitor of capacitance 2μF is connected in a circuit as shown. Both cells have emf 2.5V and internal resistance 0.5Ω. Find the charge on capacitor (in μC )
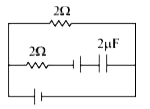
View Solution
Knowledge Check
A capacitor of capacitance 100(μ)F is charged by connecting it to a battery of emf 12 V and internal resistance 2(Ω). (a) Find the time constant of the circuit. (b) Find the time taken before 99% of maximum charge is stored on the capacitor.
A0.92msB0.4msC0.8msD0.1msAn uncharged capacitor of capacitance 8.0μF is connected to a battery of emf 6.0 V through a resistance of 24Ω, then
(i) The current in the circuit just after the connections are made is :A0.25 AB0.5 AC0.4 AD0AAn uncharged capacitor of capacitance 8.0μF is connected to a battery of emf 6.0 V through a resistance of 24Ω, then
(ii) The current in the circuit at one time constant after the connections are made is :A0.25AB0.09AC0.4AD0A
A capacitor of capacitance 8.0(μ)F is connected to a bettery of emf 6.0V through a resistance of 24(Ω).Find the current in the circuit (a)just after the connections are made and (b)one time constant after the connections are made.
View SolutionA capacitor of capacitance 10(μ)F is connected to a battery of emf 2V.It is found that it takes 50 ms for the charge on the capacitor to bacome 12.6(μ)C.find the resistance of the circuit.
View SolutionA capacitor of capacitance as C is given a charge Q. At t=0,it is connected to an ideal battery of emf (ε)through a resistance R. Find the charge on the capacitor at time t.
View SolutionAn uncharged capacitor of capacitance 8.0μF is connected to a battery of emf 6.0 V through a resistance of 24Ω, then
(ii) The current in the circuit at one time constant after the connections are made is :
View Solution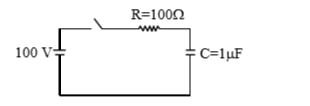
A capacitor of capacitance C=1 μF is suddenly connected to a battery of 100 volt through a resistance R=100Ω . The time taken for the capacitor to be charged to get 50 V is :
[Take ln 2 = 0.69]
View Solution
