In the circuit shown in figure E,F, G and H are cell of emf 2,1,3, and 1V respectively. The resistances 2,1,3 and 1(Omega)are their respective internal resistance .Calculate (a)the potential difference between B and D and (b) the potential differences across the terminals of each of each of the cells G and H.

2112V.
213V.
2114V.
2113V.
The correct Answer is:D
Suppose a current i_(1) goes in the branch BAD and current i_(2) in the branch DCB. The current in DB will be i_(1)-i_(2) from the junction law. The circuit with the currents shown is redrawn in figure. Applying the loop law to BADB we ge,
(2(Ω))i1−2V+1V+(1(Ω))i1+(2(Ω))(i1−i2)=0
(5(Ω))i1−(2(Ω))i2=1V....(i)
Applying the same law to the loop DCBD,we get
−3V+(3(Ω)i2+(1(Ω))i2+1V−(2(Ω))(i1−i2)=0
or,−(2(Ω))i1+(6(Ω))i2=2V....(ii)
From (i)and (ii),
i1=513A,i2=613A.
sotˆi_(1)-i_(2)=1/13A.<br>thecurrent∈BDisomB→D.<br>(a)V_(B)-V_(D)=(2(Omega)((1)/(13)A)=(2)/(13)V.<br>The potential difference across the cell G is
Vc−Vd=−(3(Ω))i2=3V.
=(3V−1813V)=2113V.
Thepotentiald⇔erenceacrossthecellHis<br>V_(C)-V_(B)=(1(Omega))i_(2)+1V=(1(Omega))((6)/(13)A+1V=(19)/(13)V.
Topper's Solved these Questions
- ELECTRIC CURRENT IN CONDUCTORSBOOK - HC VERMACHAPTER - ELECTRIC CURRENT IN CONDUCTORSEXERCISE - worked out Example
1 Videos
- ELECTRIC CURRENT IN CONDUCTORSBOOK - HC VERMACHAPTER - ELECTRIC CURRENT IN CONDUCTORSEXERCISE - Short Answer
17 Videos
- ELECTRIC CURRENT IN CONDUCTORSBOOK - HC VERMACHAPTER - ELECTRIC CURRENT IN CONDUCTORSEXERCISE - Exercises
84 Videos
- DISPERSION AND SPECTRABOOK - HC VERMACHAPTER - DISPERSION AND SPECTRAEXERCISE - Exercises
11 Videos
- ELECTRIC CURRENT THROUGH GASESBOOK - HC VERMACHAPTER - ELECTRIC CURRENT THROUGH GASESEXERCISE - Exercises
23 Videos
Similar Questions
In the circuit shown in E, F, G, and H are cells of emf 2,1,3 and 1 V, respectively. The resistances 2Ω,1Ω,3Ωand1Ω are their respectivle internal resistances.
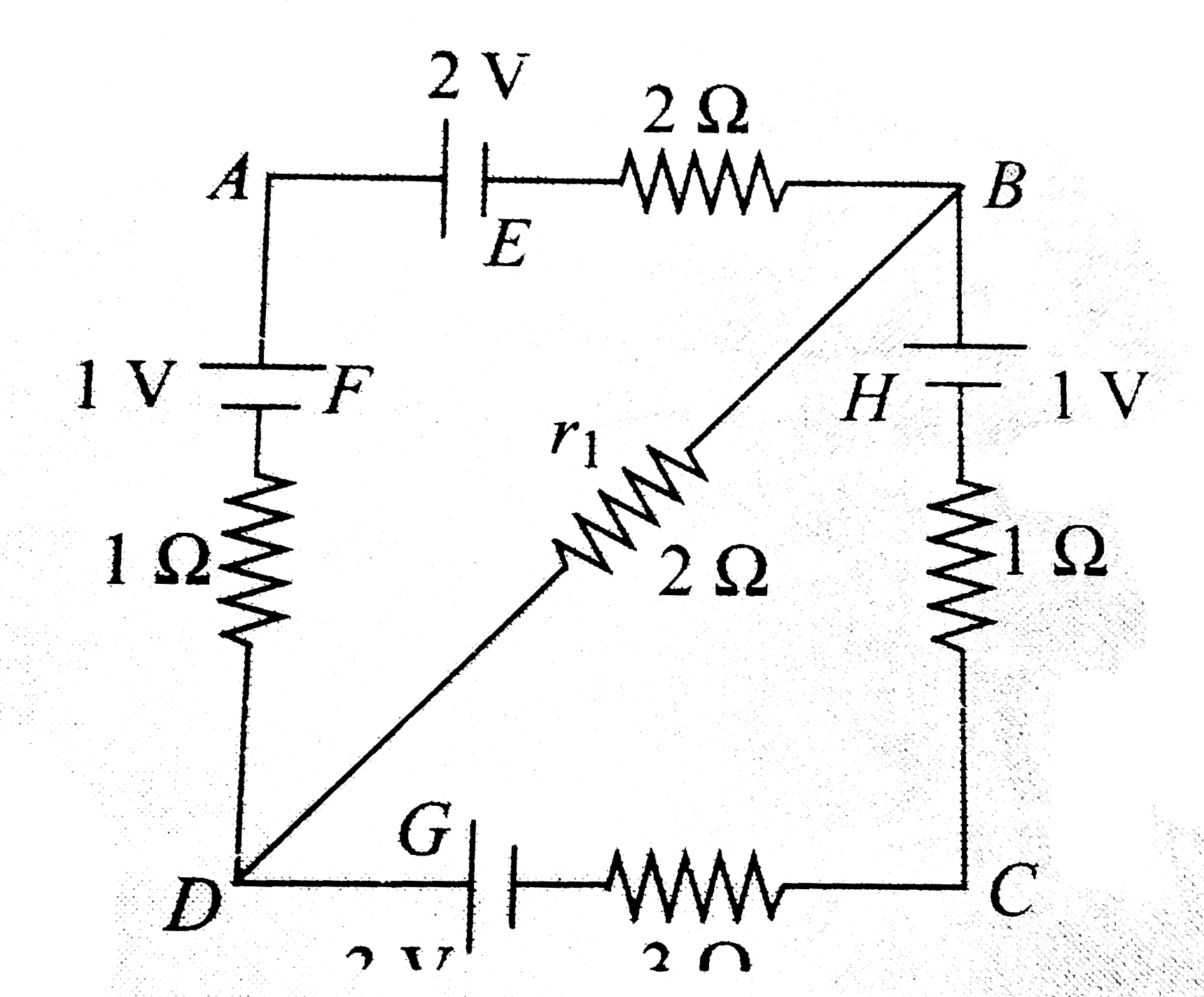
i. Find the potential difference between B and D.
(ii) Calculate the potential differences across the terminals of each of the cells G and H.
View SolutionIn the circuit shown in figure-3.159 cells E,F,G and H are of EMF 2V, 1V,3V and 1V respevitly and their internal resitance are 2Ω,1Ω,3Ω and 1Ω respectively Calculate
(a) The potential difference between points B and D
(d) The potential difference across the terminals of the cell G and H.
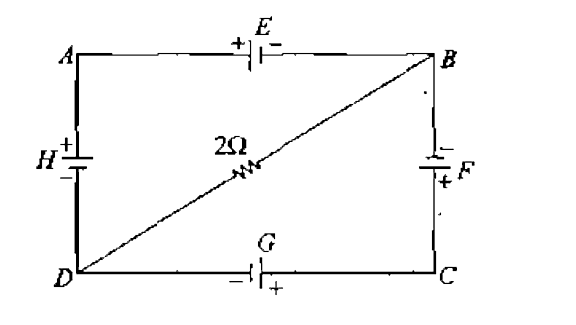
View Solution
Knowledge Check
In the circuit shown E,F,G and H are cells of emf 2V,1V,3V and 1V respectively and their internal resistance are 2Ω,1Ω,3Ω and 1Ω respectively.
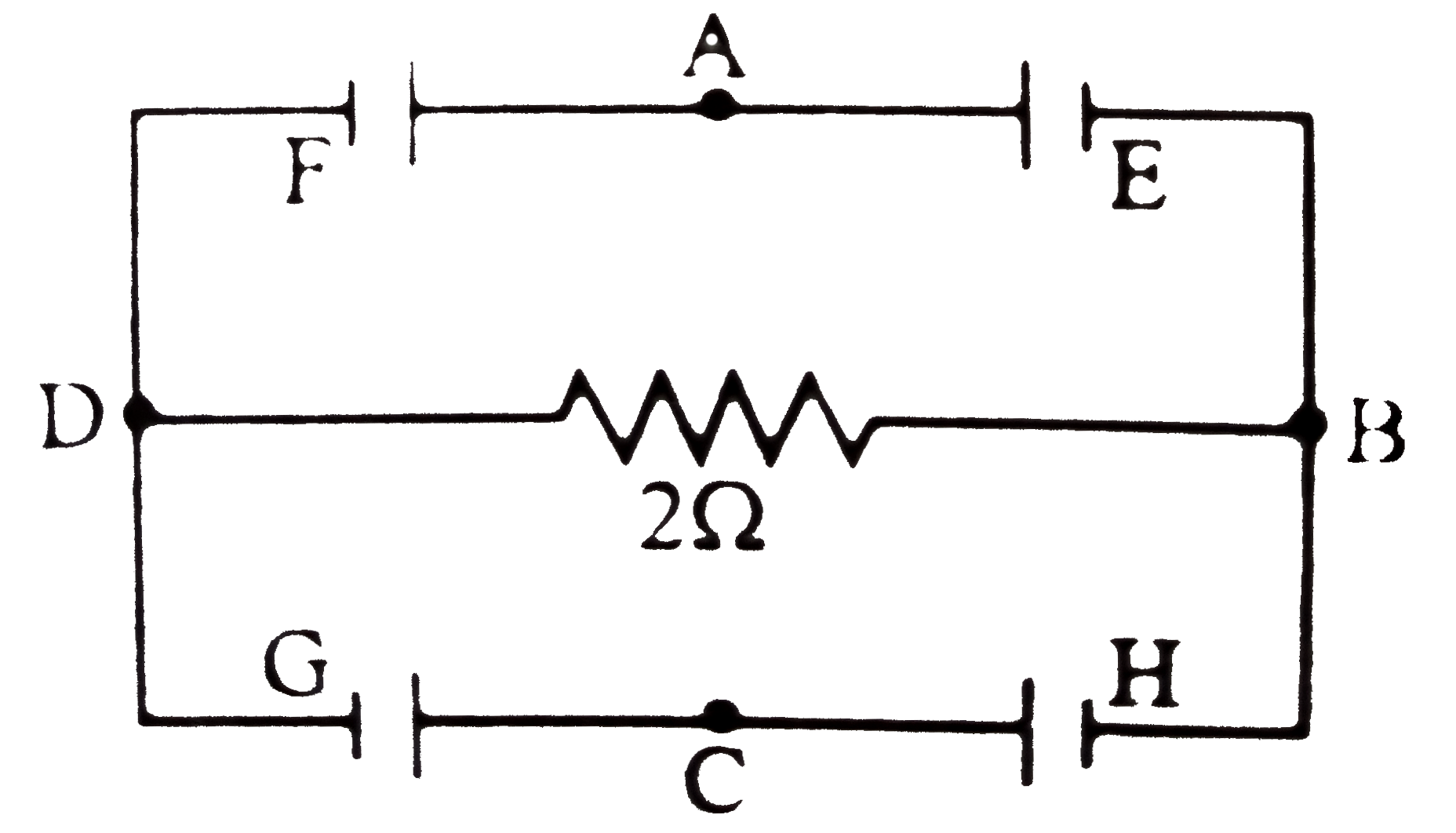 AVD−VB=−2/13VBVD−VB=2/13VCVG=21/13V=potential difference across GDVH=19/13V=potential difference across H
AVD−VB=−2/13VBVD−VB=2/13VCVG=21/13V=potential difference across GDVH=19/13V=potential difference across HIn the circuit E,F,G,Hare cell of emf 2,1,3and 1Ω respectively .The potential difference across the terminal of each of the cell G and H are
 A1.46V,1.61VB1.61V,1.46VC2.52V,1.61VD1.61V,2.25V
A1.46V,1.61VB1.61V,1.46VC2.52V,1.61VD1.61V,2.25VTwo cells A and B of e.m.f.2 V and 1.5 V respectively, are connected as shown in figure through an external resistance 10 Ω The internal resistance of each cell is 5 Ω. The potential difference EAandEB across the terminals of the cells A and B respectively are
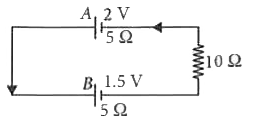 AEA=2.0v,EB=1.5VBEA=2.125V,EB=1.375VCEA=1.875V,EB=1.625VDEA=1.875V,EB=1.375V
AEA=2.0v,EB=1.5VBEA=2.125V,EB=1.375VCEA=1.875V,EB=1.625VDEA=1.875V,EB=1.375V

In the circuit shown in figure. The cells E,F,G and H have e.m.f's 2,1,3 and 1 V and internal resistance 2,1,3 and 1Ω respectively. Find the potential differences between points B and D, and across the terminals of the cells G and H.
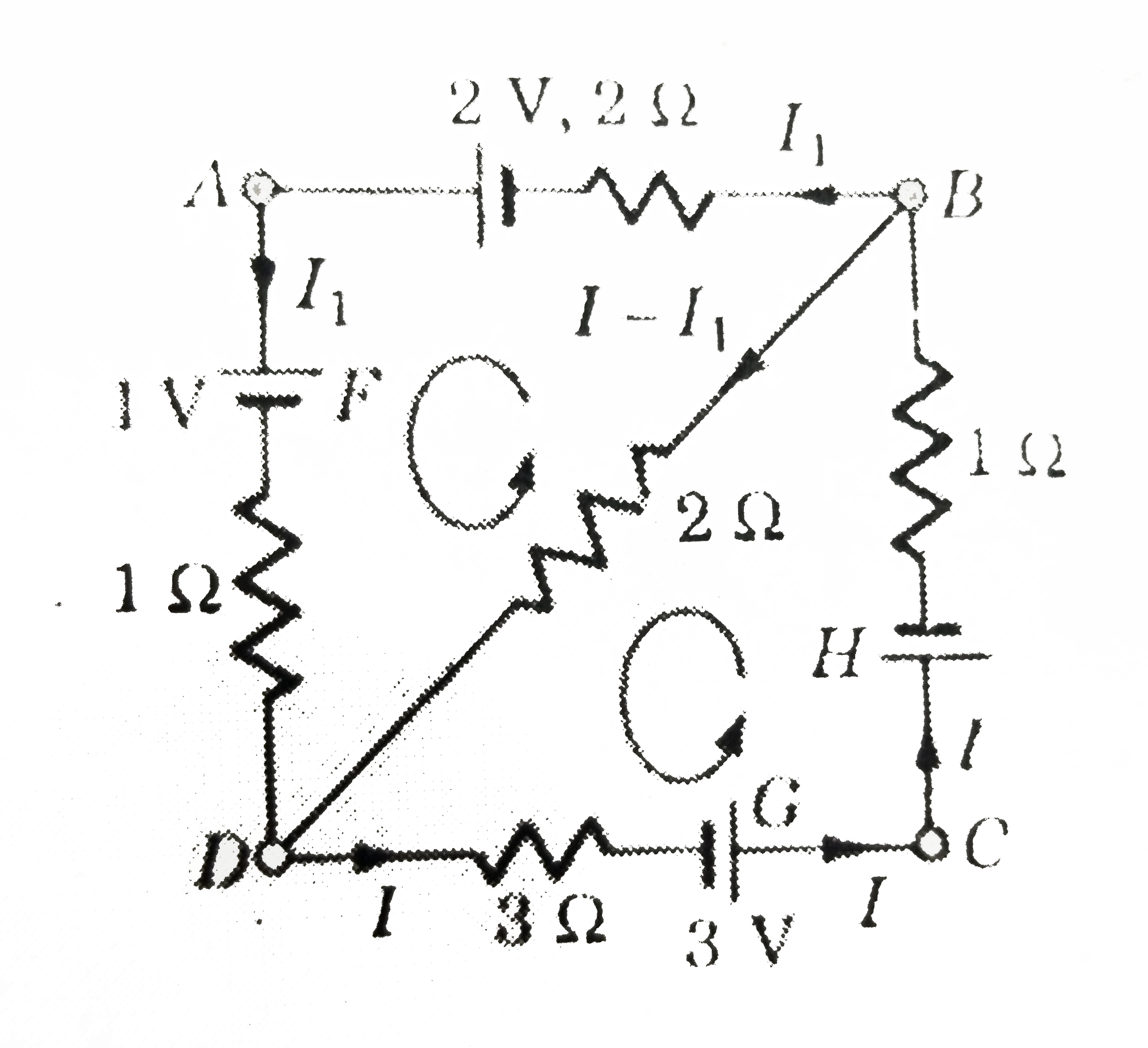
View SolutionTwo non-ideal batteries have e.m.f 2V and 8V respectively and internal resistance 1 Omega and 2 Omega respectively as shown in the figure. If the potential difference between a and b is zero then the resistance R has a value
_PHY_E01_014_Q01.png)
View SolutionA cell of emf 'E' is connected across a resistance R.The potential difference between the terminals of the cell is found to be "V" .The internal resistance of the cell must be:
View Solutionv31
View SolutionA cell of e.mf. E and internal resistance r is connected in series with an external resistance nr. Then, the ratio of the terminal potential difference to E.M.F.is
View Solution
