Two resistances R and 2R are connected in parallel in an electric circuit. The thermal energy developed in R and 2R are in the ratio
(a)1:2
(b)2:1
(c )1:4
(d)4:1
The correct Answer is:B
To find the ratio of thermal energy developed in resistances R and 2R connected in parallel, we can follow these steps:
Step 1: Understand the Circuit Configuration
- Two resistances, R and 2R, are connected in parallel across a voltage source V. In a parallel circuit, the voltage across each resistor is the same.
Step 2: Calculate Power Developed in Each Resistor
- The power (P) developed in a resistor can be calculated using the formula:
P=V2R
- For resistance R:
PR=V2R
- For resistance 2R:
P2R=V22R
Step 3: Calculate Thermal Energy Developed
- The thermal energy (E) developed in a resistor over time (t) can be calculated using the formula:
E=P⋅t
- For resistance R:
ER=PR⋅t=(V2R)⋅t=V2tR
- For resistance 2R:
E2R=P2R⋅t=(V22R)⋅t=V2t2R
Step 4: Find the Ratio of Thermal Energies
- Now, we can find the ratio of thermal energies developed in R and 2R:
Ratio=ERE2R=V2tRV2t2R
- Simplifying this gives:
Ratio=V2tR⋅2RV2t=2RR=2
Step 5: Final Ratio
- Therefore, the ratio of thermal energy developed in R to that in 2R is:
Ratio=2:1
Conclusion
The thermal energy developed in resistances R and 2R are in the ratio of 2:1.
---
- Two resistances, R and 2R, are connected in parallel across a voltage source V. In a parallel circuit, the voltage across each resistor is the same.
- The power (P) developed in a resistor can be calculated using the formula:
P=V2R
- For resistance R:
PR=V2R
- For resistance 2R:
P2R=V22R
- The thermal energy (E) developed in a resistor over time (t) can be calculated using the formula:
E=P⋅t
- For resistance R:
ER=PR⋅t=(V2R)⋅t=V2tR
- For resistance 2R:
E2R=P2R⋅t=(V22R)⋅t=V2t2R
- Now, we can find the ratio of thermal energies developed in R and 2R:
Ratio=ERE2R=V2tRV2t2R
- Simplifying this gives:
Ratio=V2tR⋅2RV2t=2RR=2
- Therefore, the ratio of thermal energy developed in R to that in 2R is:
Ratio=2:1
The thermal energy developed in resistances R and 2R are in the ratio of 2:1.
Topper's Solved these Questions
- ELECTRIC CURRENT IN CONDUCTORSBOOK - HC VERMACHAPTER - ELECTRIC CURRENT IN CONDUCTORSEXERCISE - Objective 2
9 Videos
- ELECTRIC CURRENT IN CONDUCTORSBOOK - HC VERMACHAPTER - ELECTRIC CURRENT IN CONDUCTORSEXERCISE - Exercises
84 Videos
- ELECTRIC CURRENT IN CONDUCTORSBOOK - HC VERMACHAPTER - ELECTRIC CURRENT IN CONDUCTORSEXERCISE - Short Answer
17 Videos
- DISPERSION AND SPECTRABOOK - HC VERMACHAPTER - DISPERSION AND SPECTRAEXERCISE - Exercises
11 Videos
- ELECTRIC CURRENT THROUGH GASESBOOK - HC VERMACHAPTER - ELECTRIC CURRENT THROUGH GASESEXERCISE - Exercises
23 Videos
Similar Questions
two resistors R and 2R are connected in series in an electric circuit. The thermal energy developed in R and 2R are in the ratio
View SolutionYou take two resistors of resistance 2R and 3R and connect them in parallel in an electric circuit. Calculate the ratio of electric power consumed by 2R and 3R resistors.
View Solution
Knowledge Check
Two wires having resistance R and 2 R are connected in parallel, the ratio of heat generated in 2 R and R is
A1:2B2:1C1:4D4:1Two wires with resistances R and 2 R are connected in parallel, the ratio of heat generated in 2 R and R is
A1:2B2:1C1:4D4:1In the circuit diagram,heat produces in R, 2R and 1.5R are in the ratio of
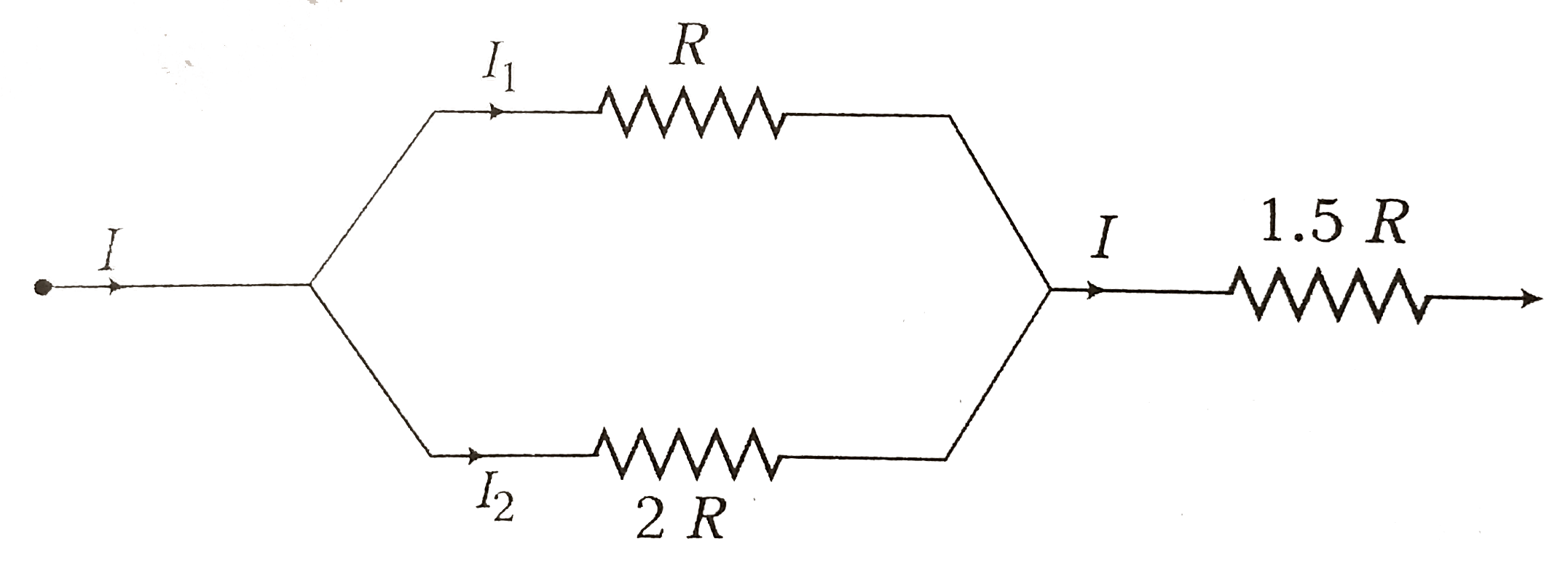 A4:2:3B8:4:27C2:4:3D27:8:4
A4:2:3B8:4:27C2:4:3D27:8:4
If two resistors of R1 and R2 ohms are connected in parallel in an electric circuit to make an R ohm resistor, the value of R can be found from the equation,
1R=1R1+1R2
If R1 is decreasing at the rate of 1 ohm/sec and R2 i increasing at the rate of 0.5 ohm/sec, at what rate is R changing when R1=75 ohm and R2=50 ohm ?

View SolutionMake sure that the current distribution over two resistances R1 and R2 connnected in parallel corresponds to the minimum thermal power generated in this circuit.
View SolutionWhen two resistors of resistances R1andR2 are connected in parallel, the net resistance is 3Ω. When connected in series, its value is 16Ω. Calculate the values of R1andR2.
View SolutionIf resistors of resistance R1 and R2 are connected in parallel,then resultant resistance is "
View SolutionTwo lamps have resistance r and R, R being greater than r. If they are connected in paralled in an electric circuit, then
View Solution
