A magnetic field of (4.0X10−3→k) T exerts a force of (4.0→i+3.0→jx10−10 N on a particle having a charge of 1.0X10−9 C and going in the x-y plane. Find the velocity of the particle.
To find the velocity of the particle in the given magnetic field, we can use the formula for the magnetic force acting on a charged particle moving in a magnetic field. The force →F is given by:
→F=q(→v×→B)
where:
- →F is the magnetic force,
- q is the charge of the particle,
- →v is the velocity of the particle,
- →B is the magnetic field.
Step 1: Identify the given values
- Magnetic field →B=4.0×10−3^kT
- Force →F=(4.0^i+3.0^j)×10−10N
- Charge q=1.0×10−9C
Step 2: Assume the velocity vector
Assume the velocity of the particle is given by:
→v=vx^i+vy^j
Step 3: Calculate the cross product →v×→B
Using the right-hand rule for the cross product, we can calculate:
→v×→B=(vx^i+vy^j)×(4.0×10−3^k)
Using the properties of cross products:
^i×^k=^j,^j×^k=−^i
Thus, we have:
→v×→B=vx(4.0×10−3^j)−vy(4.0×10−3^i)=4.0×10−3vx^j−4.0×10−3vy^i
Step 4: Substitute into the force equation
Now substituting this into the force equation:
→F=q(→v×→B)=(1.0×10−9)(4.0×10−3vx^j−4.0×10−3vy^i)
This simplifies to:
→F=(4.0×10−12vy^i+4.0×10−12vx^j)
Step 5: Equate components of the force
Now we can equate the components of the force:
1. For the ^i component:
−4.0×10−12vy=4.0×10−10
vy=−4.0×10−104.0×10−12=−100m/s
2. For the ^j component:
4.0×10−12vx=3.0×10−10
vx=3.0×10−104.0×10−12=75m/s
Step 6: Write the final velocity vector
Thus, the velocity vector of the particle is:
→v=75^i−100^jm/s
Final Answer
The velocity of the particle is:
→v=75^i−100^jm/s
---
- →F is the magnetic force,
- q is the charge of the particle,
- →v is the velocity of the particle,
- →B is the magnetic field.
- Magnetic field →B=4.0×10−3^kT
- Force →F=(4.0^i+3.0^j)×10−10N
- Charge q=1.0×10−9C
Assume the velocity of the particle is given by:
Using the right-hand rule for the cross product, we can calculate:
Now substituting this into the force equation:
Now we can equate the components of the force:
−4.0×10−12vy=4.0×10−10
vy=−4.0×10−104.0×10−12=−100m/s
4.0×10−12vx=3.0×10−10
vx=3.0×10−104.0×10−12=75m/s
Thus, the velocity vector of the particle is:
The velocity of the particle is:
Topper's Solved these Questions
Similar Questions
A magnetic field of 8ˆkmT exerts a force of (4.0ˆi+3.0ˆj)×10−10N on a particle having a charge of 5×10−10C and going in the X−Y plane.Find the velocity of the particle.
View SolutionA magnetic field of (4.0×10−3ˆk)T exerts a force (4.0ˆi+3.0ˆj)×10−10N on a particle having a charge 10−9C and moving in te x−y plane. Find the velocity of the particle.
View Solution
Knowledge Check
A magnetic field 4×10−3 kT exerts a force (4ˆI+3ˆj)×1010 N on a particle having a charge 10−9 C and going on the XY plane The velocity of the particle is
A−75ˆI+100ˆjB−100ˆI+75ˆjC25ˆI+2ˆjD2ˆI+25ˆivx is the velocity of a particle moving along the x-axis as shown in the figure. If x=2.0m at t=1.0s, what is the position of the particle at t=6.0s ?
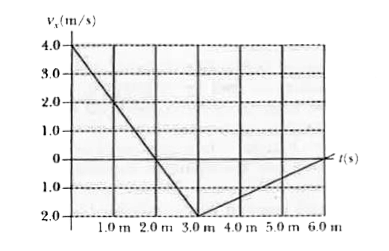 A−2.0 mB+2.0 mC+1.0 mD−1.0 m
A−2.0 mB+2.0 mC+1.0 mD−1.0 mMagnetic force on a charged particle is given by →Fm=q(→v×→B) and electrostatic force →Fe=q→E. A particle having charge q = 1C and mass 1 kg is released from rest at origin. There are electric and magnetic field given by →E=(10ˆi)N/Cforx=1.8m and →B=−(5ˆk)T for 1.8m≤x≤2.4m
A screen is placed parallel to y-z plane at x=3m. Neglect gravity forces.
The speed with which the particle will collide the screen isA3ms−1B6m/s−1C9 m//s^(-1)D12m/s−1
A particle moves in the x−y plane such that its coordinates are given x=10√3t,y=10t−t2 and t is time, find the initial velocity of the particle.
View SolutionA uniform magnetic field of magnitude 0.20 T exists in space from east to west what speed should a particle of mass 0.010 g and having a charge 1.0×10−5C be projected from south to north so that it moves with a uniform velocity?
View SolutionA particle having a charge of 2.0X10−8C and a mass of 2.0X10−10g is projected with a speed of 2.0X103ms−1 in a region having a uniform magnetic field of 0.10 T. The velocity is perpendicular to the field. Find the radius of the circle formed by the particle and also the time period.
View SolutionAn experimenter's diary reads as follows: ''a charged particle is projected in a magnetic feld of (7.0→i−3.0→j)X10−3 T. The acceleraation of the particle is found to be (sqrare→i+7.0→j)X10−6ms−2'.Theνmber→the≤ftofvec i in the last expression was not readable. What can this number be?
View SolutionVx is the velocity of a particle of a particle moving along the x−axis as shown. If x=2.0m at t=1.0s, what is the position of the particle at t=6.0s?

View Solution
