In Ampere's law (∮(→B).(→dl))=(μ0)I, the current outside the curve is not included on the right hand side. Does it mean that the magnetic field B calculated by using Ampere's law , gives the contribution of only the currents crossing the area bounded by the curve?
Step by step video & image solution for In Ampere's law (oint (vec B).(vec dl))=(mu_0)I, the current outside the curve is not included on the right hand side. Does it mean that the magnetic field B calculated by using Ampere's law , gives the contribution of only the currents crossing the area bounded by the curve? by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- MAGNETIC FIELD DUE TO CURRENTBOOK - HC VERMACHAPTER - MAGNETIC FIELD DUE TO CURRENTEXERCISE - Objective 1
12 Videos
- MAGNETIC FIELD DUE TO CURRENTBOOK - HC VERMACHAPTER - MAGNETIC FIELD DUE TO CURRENTEXERCISE - Objective 2
7 Videos
- MAGNETIC FIELD DUE TO CURRENTBOOK - HC VERMACHAPTER - MAGNETIC FIELD DUE TO CURRENTEXERCISE - Worked Out Examples
15 Videos
- MAGNETIC FIELDBOOK - HC VERMACHAPTER - MAGNETIC FIELDEXERCISE - Exercises
61 Videos
- MAGNETIC PROPERTIES OF MATTERBOOK - HC VERMACHAPTER - MAGNETIC PROPERTIES OF MATTEREXERCISE - Exercises
9 Videos
Similar Questions
A current circular conducting loop exerts a magnetic field both inside and outside it. The magnetic field at the cetre of a current loop of radius 'R' and carrying a current I is given as :
B=μ0I2R
The magnetic field lines due to a circular current loop form closed loops. The direction of the magnetic field is given by the right hand thumb rule, which states that if one curls the palm of his right hand around the current loop with the fingers pointing in the direction of the current, the right hand thumb will give the direction of the magnetic field. From this law it is clear that the direction of magnetic field →B is always perpendicular to the direction of flow of current or perpendicular to the plane of circular current loop.
Draw the magnetic field lines due to a circular current loop placed in a horizontal plane.
An enamelled copper wire of length L is bent in the form of a circular loop and a curretn I is passed through it so that a magnetic field B is get up at its centre. Now the same wire is bent in the form of a circular coil having N turns and same current I is passed through it. What is the magnetic field develop at the centre of this coil?
View SolutionA current circular conducting loop exerts a magnetic field both inside and outside it. The magnetic field at the cetre of a current loop of radius 'R' and carrying a current I is given as :
B=μ0I2R
The magnetic field lines due to a circular current loop form closed loops. The direction of the magnetic field is given by the right hand thumb rule, which states that if one curls the palm of his right hand around the current loop with the fingers pointing in the direction of the current, the right hand thumb will give the direction of the magnetic field. From this law it is clear that the direction of magnetic field →B is always perpendicular to the direction of flow of current or perpendicular to the plane of circular current loop.
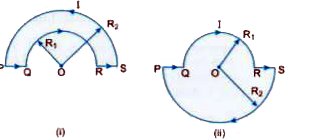
Determine the magnetic field at the centre point O due to two concentric semicircular loops of radii R1andR2 carrying a current I, when the loops of radii R1andR2 carrying a current I, when the loops are arranged as shown in Fig.
View Solution
Knowledge Check
Ampere's law provides us an easy way to calculate the magnetic field due to a symmetrical distribution of current. Its mathemfield expression is ∮→B.dl=μ0Iin.
The quantity on the left hand side is known as line as integral of magnetic field over a closed Ampere's loop.
In the above question, find the magnetic field induction at a point distance r from the axis when rgta. Assume relative permeability of the medium surrounding the conductor to be unity.Aμ0ka44rBμ0kr32Cμ0kπa42rDμ0ka34Ampere's law provides us an easy way to calculate the magnetic field due to a symmetrical distribution of current. Its mathemfield expression is ∮→B.dl=μ0Iin.
The quantity on the left hand side is known as line as integral of magnetic field over a closed Ampere's loop.
If the current density in a linear conductor of radius a varies with r according to relation J=kr2, where k is a constant and r is the distance of a point from the axis of conductor, find the magnetic field induction at a point distance r from the axis when rlta. Assume relative permeability of the conductor to be unity.Aμ0ka44rBμ0kr32Cμ0kπa42rDμ0ka34Ampere's law provides us an easy way to calculate the magnetic field due to a symmetrical distribution of current. Its mathematical expression is ∮→B.dl=μ0Iin.
The quantity on the left hand side is known as line as integral of magnetic field over a closed Ampere's loop.
Only the current inside the Amperian loop contributes inAfinding magnetic field at any point on the Ampere's loopBline integral of magnetic fieldCin both of the aboveDin neither of them
A current circular conducting loop exerts a magnetic field both inside and outside it. The magnetic field at the cetre of a current loop of radius 'R' and carrying a current I is given as :
B=μ0I2R
The magnetic field lines due to a circular current loop form closed loops. The direction of the magnetic field is given by the right hand thumb rule, which states that if one curls the palm of his right hand around the current loop with the fingers pointing in the direction of the current, the right hand thumb will give the direction of the magnetic field. From this law it is clear that the direction of magnetic field →B is always perpendicular to the direction of flow of current or perpendicular to the plane of circular current loop.
Does a charge at rest produes a magnetic field around it?
View SolutionA current circular conducting loop exerts a magnetic field both inside and outside it. The magnetic field at the cetre of a current loop of radius 'R' and carrying a current I is given as :
B=μ0I2R
The magnetic field lines due to a circular current loop form closed loops. The direction of the magnetic field is given by the right hand thumb rule, which states that if one curls the palm of his right hand around the current loop with the fingers pointing in the direction of the current, the right hand thumb will give the direction of the magnetic field. From this law it is clear that the direction of magnetic field →B is always perpendicular to the direction of flow of current or perpendicular to the plane of circular current loop.
Draw the magnetic field lines due to a circular current loop placed in a horizontal plane.
View SolutionA current circular conducting loop exerts a magnetic field both inside and outside it. The magnetic field at the cetre of a current loop of radius 'R' and carrying a current I is given as :
B=μ0I2R
The magnetic field lines due to a circular current loop form closed loops. The direction of the magnetic field is given by the right hand thumb rule, which states that if one curls the palm of his right hand around the current loop with the fingers pointing in the direction of the current, the right hand thumb will give the direction of the magnetic field. From this law it is clear that the direction of magnetic field →B is always perpendicular to the direction of flow of current or perpendicular to the plane of circular current loop.

How is the magnetic field at O modified when the two loops are rearranged as shown in Fig.
View SolutionA rectangular coil of sides l and b carrying a current I is subjected to a uniform magnetic field →B acting perpendicular to its plane. Obtain the expression for the torque acting on it.
View SolutionAssertion: A current I flows I flows along the length of an infinitely long straight and thin walled pipe. Then the magnetic field at any point inside the pipe is zero.
Reason: ∮→B.d→l=μI
View Solution
