Two long, straight wires, each carrying a current of 5A, are placed along the x and y axes respectively. The currents point along the positive directions of the axes. Find the magnetic fields at the points (a) (1m, 1m), (b) (-1m, 1m), (c) (-1m, -1m) and (d) (1m, -1m).
To find the magnetic fields at the specified points due to two long, straight wires carrying currents of 5 A along the x and y axes, we will use the formula for the magnetic field created by a long straight wire:
B=μ0I2πd
where:
- B is the magnetic field,
- μ0 is the permeability of free space (4π×10−7T m/A),
- I is the current (5 A in this case),
- d is the perpendicular distance from the wire to the point where the magnetic field is being calculated.
1. Determine the Magnetic Field at Point (1m, 1m):
- For the wire along the x-axis (current in the positive x direction):
- The distance d from the wire to the point (1, 1) is 1 m (the y-coordinate).
- The magnetic field Bx due to the x-axis wire is:
Bx=μ0I2πd=(4π×10−7T m/A)⋅52π⋅1=20×10−72=10×10−7T=1×10−6T
- The direction of Bx at (1, 1) is out of the page (using the right-hand rule).
- For the wire along the y-axis (current in the positive y direction):
- The distance d from the wire to the point (1, 1) is also 1 m (the x-coordinate).
- The magnetic field By due to the y-axis wire is:
By=μ0I2πd=(4π×10−7T m/A)⋅52π⋅1=10×10−7T=1×10−6T
- The direction of By at (1, 1) is into the page.
- The net magnetic field at (1, 1) is:
Bnet=Bx−By=1×10−6−1×10−6=0T
2. Determine the Magnetic Field at Point (-1m, 1m):
- For the wire along the x-axis:
- The distance d is still 1 m.
- The magnetic field Bx is the same as before:
Bx=1×10−6T(out of the page)
- For the wire along the y-axis:
- The distance d is still 1 m.
- The magnetic field By is still:
By=1×10−6T(into the page)
- The net magnetic field at (-1, 1) is:
Bnet=Bx−By=1×10−6−1×10−6=0T
3. Determine the Magnetic Field at Point (-1m, -1m):
- For the wire along the x-axis:
- The distance d is still 1 m.
- The magnetic field Bx is:
Bx=1×10−6T(out of the page)
- For the wire along the y-axis:
- The distance d is still 1 m.
- The magnetic field By is:
By=1×10−6T(out of the page)
- The net magnetic field at (-1, -1) is:
Bnet=Bx+By=1×10−6+1×10−6=2×10−6T(out of the page)
4. Determine the Magnetic Field at Point (1m, -1m):
- For the wire along the x-axis:
- The distance d is still 1 m.
- The magnetic field Bx is:
Bx=1×10−6T(out of the page)
- For the wire along the y-axis:
- The distance d is still 1 m.
- The magnetic field By is:
By=1×10−6T(out of the page)
- The net magnetic field at (1, -1) is:
Bnet=Bx+By=1×10−6+1×10−6=2×10−6T(out of the page)
Summary of Results:
- At (1m, 1m): B=0T
- At (-1m, 1m): B=0T
- At (-1m, -1m): B=2×10−6T (out of the page)
- At (1m, -1m): B=2×10−6T (out of the page)
- B is the magnetic field,
- μ0 is the permeability of free space (4π×10−7T m/A),
- I is the current (5 A in this case),
- d is the perpendicular distance from the wire to the point where the magnetic field is being calculated.
- For the wire along the x-axis (current in the positive x direction):
- The distance d from the wire to the point (1, 1) is 1 m (the y-coordinate).
- The magnetic field Bx due to the x-axis wire is:
Bx=μ0I2πd=(4π×10−7T m/A)⋅52π⋅1=20×10−72=10×10−7T=1×10−6T
- The direction of Bx at (1, 1) is out of the page (using the right-hand rule).
- For the wire along the y-axis (current in the positive y direction):
- The distance d from the wire to the point (1, 1) is also 1 m (the x-coordinate).
- The magnetic field By due to the y-axis wire is:
By=μ0I2πd=(4π×10−7T m/A)⋅52π⋅1=10×10−7T=1×10−6T
- The direction of By at (1, 1) is into the page.
- The net magnetic field at (1, 1) is:
Bnet=Bx−By=1×10−6−1×10−6=0T
- For the wire along the x-axis:
- The distance d is still 1 m.
- The magnetic field Bx is the same as before:
Bx=1×10−6T(out of the page)
- For the wire along the y-axis:
- The distance d is still 1 m.
- The magnetic field By is still:
By=1×10−6T(into the page)
- The net magnetic field at (-1, 1) is:
Bnet=Bx−By=1×10−6−1×10−6=0T
- For the wire along the x-axis:
- The distance d is still 1 m.
- The magnetic field Bx is:
Bx=1×10−6T(out of the page)
- For the wire along the y-axis:
- The distance d is still 1 m.
- The magnetic field By is:
By=1×10−6T(out of the page)
- The net magnetic field at (-1, -1) is:
Bnet=Bx+By=1×10−6+1×10−6=2×10−6T(out of the page)
- For the wire along the x-axis:
- The distance d is still 1 m.
- The magnetic field Bx is:
Bx=1×10−6T(out of the page)
- For the wire along the y-axis:
- The distance d is still 1 m.
- The magnetic field By is:
By=1×10−6T(out of the page)
- The net magnetic field at (1, -1) is:
Bnet=Bx+By=1×10−6+1×10−6=2×10−6T(out of the page)
- At (1m, 1m): B=0T
- At (-1m, 1m): B=0T
- At (-1m, -1m): B=2×10−6T (out of the page)
- At (1m, -1m): B=2×10−6T (out of the page)
Topper's Solved these Questions
- MAGNETIC FIELD DUE TO CURRENTBOOK - HC VERMACHAPTER - MAGNETIC FIELD DUE TO CURRENTEXERCISE - Objective 2
7 Videos
- MAGNETIC FIELDBOOK - HC VERMACHAPTER - MAGNETIC FIELDEXERCISE - Exercises
61 Videos
- MAGNETIC PROPERTIES OF MATTERBOOK - HC VERMACHAPTER - MAGNETIC PROPERTIES OF MATTEREXERCISE - Exercises
9 Videos
Similar Questions
A current of 10A is established in a long wire along the positive z-axis. Find the magnetic field (vec B) at the point (1m , 0 , 0).
View SolutionAn infinitely long time charge has linear charge density λC/m the line charge is along the line x=0,z=2m find the electric field at point (1,1,1) m.
View Solution
Knowledge Check
Two parallel wires carrying current 1 A and 3 A respectively are 1 m apart. If the current is in opposite direction, the force per unit length on both the wires will be:
A6×10−5 repulsiveB6×10−5Nm attractiveC6×10−7Nm repulsiveD6×10−5Nm attractiveA conductor of length 1m and carrying current of 1A is placed at an angle 45∘ to the magnetic field of 1 oersted. The force acting on the conductor is
A10−4√2NB10−4√3NC10−2√3ND10−2√2NTwo long parallel wires carrying equal current separated by 1m, exert a force of 2×10−7N//m on one another. The current flowing through them is
A2.0AB2.0×10−7AC1.0AD1.0×10−7A
A conductor of length 1m and carrying current of 1A is placed parallel to the magnetic field of 1gauss.The magnetic force acting on the conductor is: ?
View SolutionA wire of length 2 m carrying a current of 1 A is bend to form a circle. The magnetic moment of the coil is (in A−m2)
View SolutionA current carrying power line carries current from west to east. The direction of magnetic field 1m above is
View SolutionThree infinitely long wires, each carrying a current 1A, are placed such that one end of each wire is at the origin, and, one of these wires is along x-axis, the other along y-axis and the third along z-axis. Magnetic induction at point (-2 m, 0, 0) due to the system of these wires can be expressed as
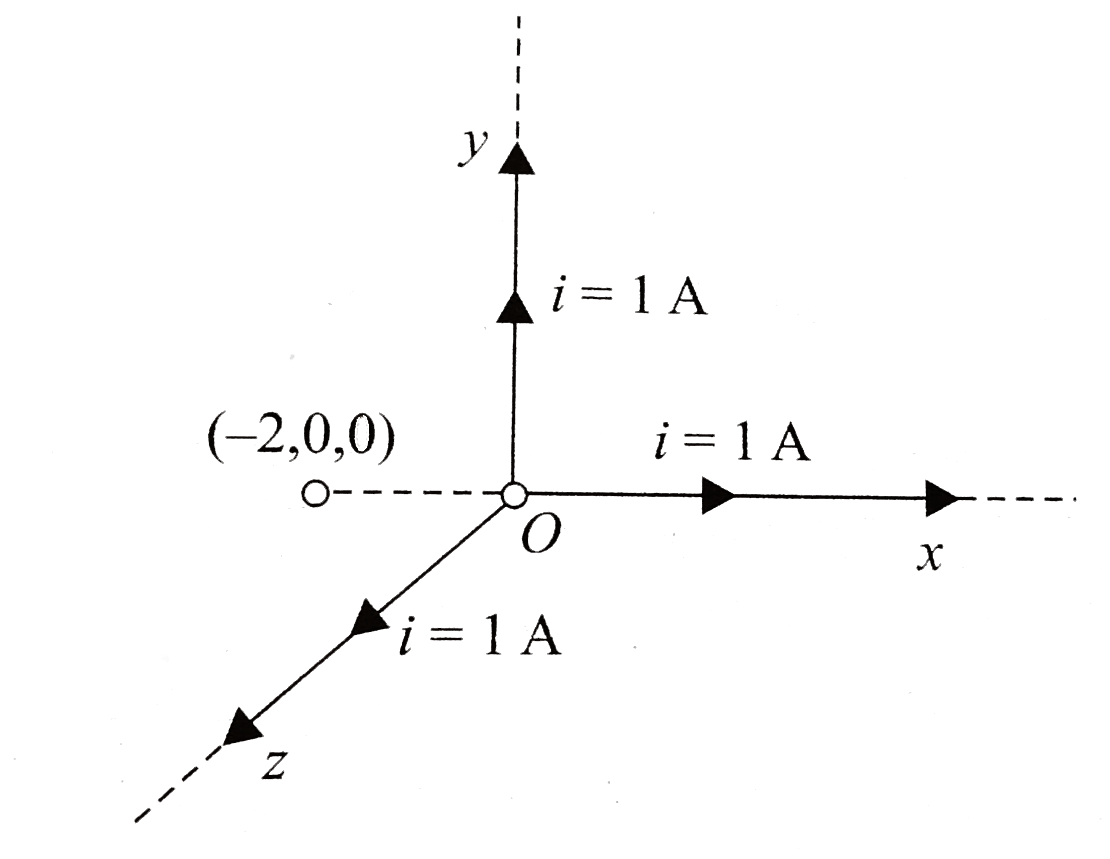
View SolutionAs charge q=1μC is placed at point (1m,2m,4m). Find the electric field at point P(0,−4m,3m)
View Solution
