A galvanometer coil has a resistance of 100Ω. When a current passes through the galvanometer, 1% of the current goes through the coil and the rest through the shunt. Find the resistance of the shunt.
The situation is shown in figure. As the potential differences the 100Ω coil and across the shunt Rs are the same,
0.01I×100Ω=0.99I×Rs
or, R_s = (0.01 xx 100)/(0.99) Omega = 100/99 Omega.

Topper's Solved these Questions
- PERMANENT MAGNETSBook:HC VERMAChapter:PERMANENT MAGNETSExercise:Short Answer
Explore 11 Videos
- PERMANENT MAGNETSBook:HC VERMAChapter:PERMANENT MAGNETSExercise:Objective 1
Explore 13 Videos
- PERMANENT MAGNETSBook:HC VERMAChapter:PERMANENT MAGNETSExercise:Exercises
Explore 25 Videos
- OPTICAL INSTRUMENTSBook:HC VERMAChapter:OPTICAL INSTRUMENTSExercise:Exercises
Explore 23 Videos
- PHOTO ELECTRIC EFFECT AND WAVE PARTICLE DUALITYBook:HC VERMAChapter:PHOTO ELECTRIC EFFECT AND WAVE PARTICLE DUALITYExercise:Exercise
Explore 2 Videos
Similar Questions
A galvanometer coil has a resistance G. 1% of the total current goes through the coil and rest through the shunt. What is the resistance of the shunt in terms of G?
View SolutionA galvanometer has a resistance of 98Ω. If 2% of the main current is to be passed through the meter, what should be the value of the shunt ?
View Solution
Knowledge Check
A galvanometer has a resistance of 49Ω.If 2% of the main current is to be passed through the meter, The value of the shunt will be
A2ΩB1ΩC12ΩD14ΩA galvanometer of coil resistance 100Ω is connected to a shunt of resistance 10Ω . The current through the galvanometer is i1 , the current through the shunt is i2 and the total current into the combination is i3 , then the ratio i1:i2:i3 is
A1:10:11B10:1:11C11:10:1D10:11:1A galvanometer has a resistance of 3663Ω. A shunt Sis connected across it such that (1/34) of the total current passes through the galvanometer. Then the value of the shunt is :
A222ΩB111ΩC11ΩD22Ω
If the resistance of the galvanometer G is 15Ω, then current through the galvanometer will be
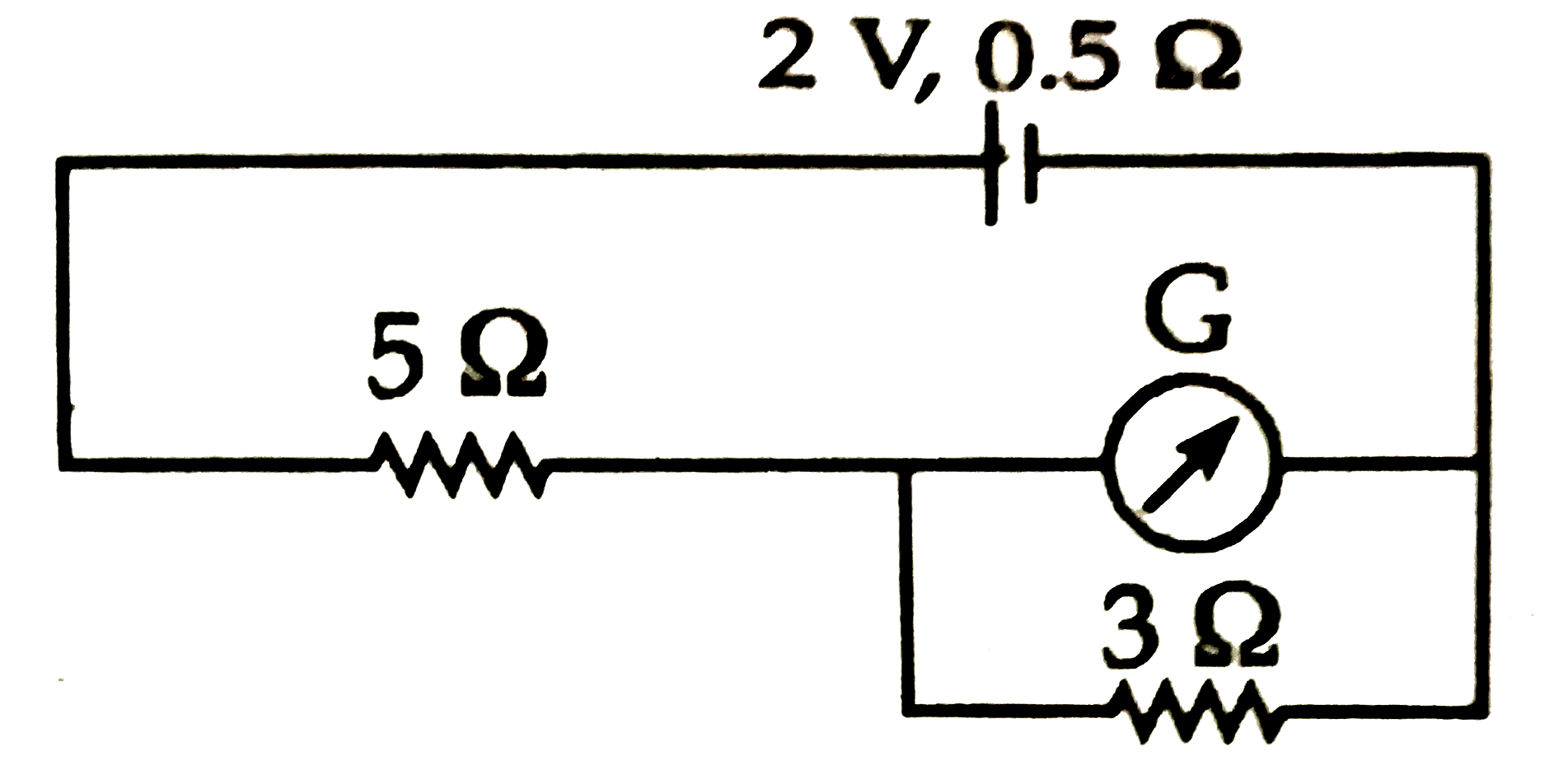
View SolutionA galvanomter of resistance 50Ω is shunted by a resistance of 5Ω. What fraction of the main current passes through the galvanometer? Through the shunt?
View SolutionA36Ω galvanometer is shunted by resistance of 4Ω. The percentage of the total current, which passes through the galvanometer is
View SolutionA 36Ω galvanometer is shunted by resistance of 4Ω. The percentage of the total current, which passes through the galvanometer is
View SolutionA galvanometer has a resistance of 3663Ω. A shunt S is connected across it such that (1/34) of the total current passes through the galvanometer. Then the value of the shunt (in Ω) is
View Solution