Shows a horizontal magnetic field which is uniform above the dotted line and is zero below it. A long, rectangular, conducting loop of width L, mass m and resistance R is placed partly above and partly below the dotted line with the lower edge parallel to it . with what velocity should it be pushed downwards so that it may continue ot fall without any acceleration?

Let the uniform velocity of fall be v
The emf is indcued across the upper wire and its magnitude is ε=vBl<br>Thecurrent∈duced∈theameis i=(vBl)/(R )sotˆ,themag≠ticforceontheupperarmisF = ilB = (vB^2l^2)/(R )
This force is in the upward direction
As the frame falls uniformly, this force should balance its weight
Thus, mg=vB2l2R or, v=mgRB2l2
Topper's Solved these Questions
- ELECTROMAGNETIC INDUCTIONBook:HC VERMAChapter:ELECTROMAGNETIC INDUCTIONExercise:Short Answer
Explore 13 Videos
- ELECTROMAGNETIC INDUCTIONBook:HC VERMAChapter:ELECTROMAGNETIC INDUCTIONExercise:Objective 1
Explore 12 Videos
- ELECTROMAGNETIC INDUCTIONBook:HC VERMAChapter:ELECTROMAGNETIC INDUCTIONExercise:EXERCISE
Explore 9 Videos
- ELECTRIC FIELD AND POTENTIALBook:HC VERMAChapter:ELECTRIC FIELD AND POTENTIALExercise:Exercises
Explore 75 Videos
- ELECTROMAGNETIC WAVESBook:HC VERMAChapter:ELECTROMAGNETIC WAVESExercise:Exercises
Explore 9 Videos
Similar Questions
Fig. 12.32 shows a long, rectangular, conducting loop of with l, mass m and resistance R placed partly in a perpendicular magnetic field B. With what velocity should it be pushed downwards so that it may continue to fall wihtout any acceleration?
View SolutionA pair of parallel horizontal conducting rails of negligible resistance shorted at one end is fixed on a table. The distance between the rails is L. A conducting massless rod of resistance R can slide on the rails frictionlessly. The rod is tied to a massless string which passes over a pulley fixed to the edge of the table, A mass m, tied to the other end of the string hanges vertically. A constant magnetic field B exists perpendicular to the table. If the system is released from rest, calculate.
(i) the terminal velocity achieved by the rod, and
the acceleration of the mass at the instant when the velocity of the rod is half the terminal velocity.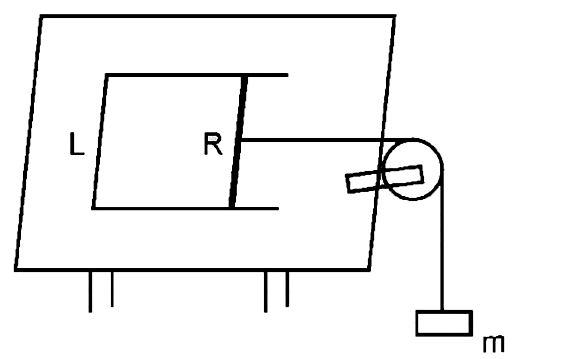
View Solution
Knowledge Check
Consider a perfectly conducting uniform disc of mass m and radius 'a' hinged in a vertical plane from its centre and free to rotate with respect to hinge. A resistance R is connected between centre of the disc annd periphery by using two sliding contacts C1 & C2. A long non -conducting massless string is wrapped around the disk, whose another end is attached with a block of mass m. There exists a uniform horizontal magnetic field B, whose arrangement is shown in figure.

Given system is released from rest at t=0. Assume friction between string and disc is sufficient so that there is no slipping between them let at any instant t, velocity of block is v, angular velocity of the disc is ω and current in resistance is i
Just after t=0 the acceleration of block is:AgBg2C2g3Dg5Sphere of mass M and radius R is kept on a rough horizontal floor. A small particle of mass m, moving horizontally with velocity, collides with the sphere and sticks to it. Line of motion of particle before collision is at a heighth above the floor. Assume that mase of sphere is very large in comparison to particle so that we may assume that centre of mass of the combined system remains at the centre of the sphere after the collision.

At what height h above the floor, particle should hit the sphere so that it may start pure rolling after the collision.A5R7B3R5C3R7D7R5A long solenoid having n = 200 turns per metre has a circular cross-section of radius a1=1cm. A circular conducting loop of radius a2=4cm and resistance R=5(Ω) encircles the solenoid such that the centre of circular loop coincides with the midpoint of the axial line of the solenoid and they have the same axis as shown in Fig.
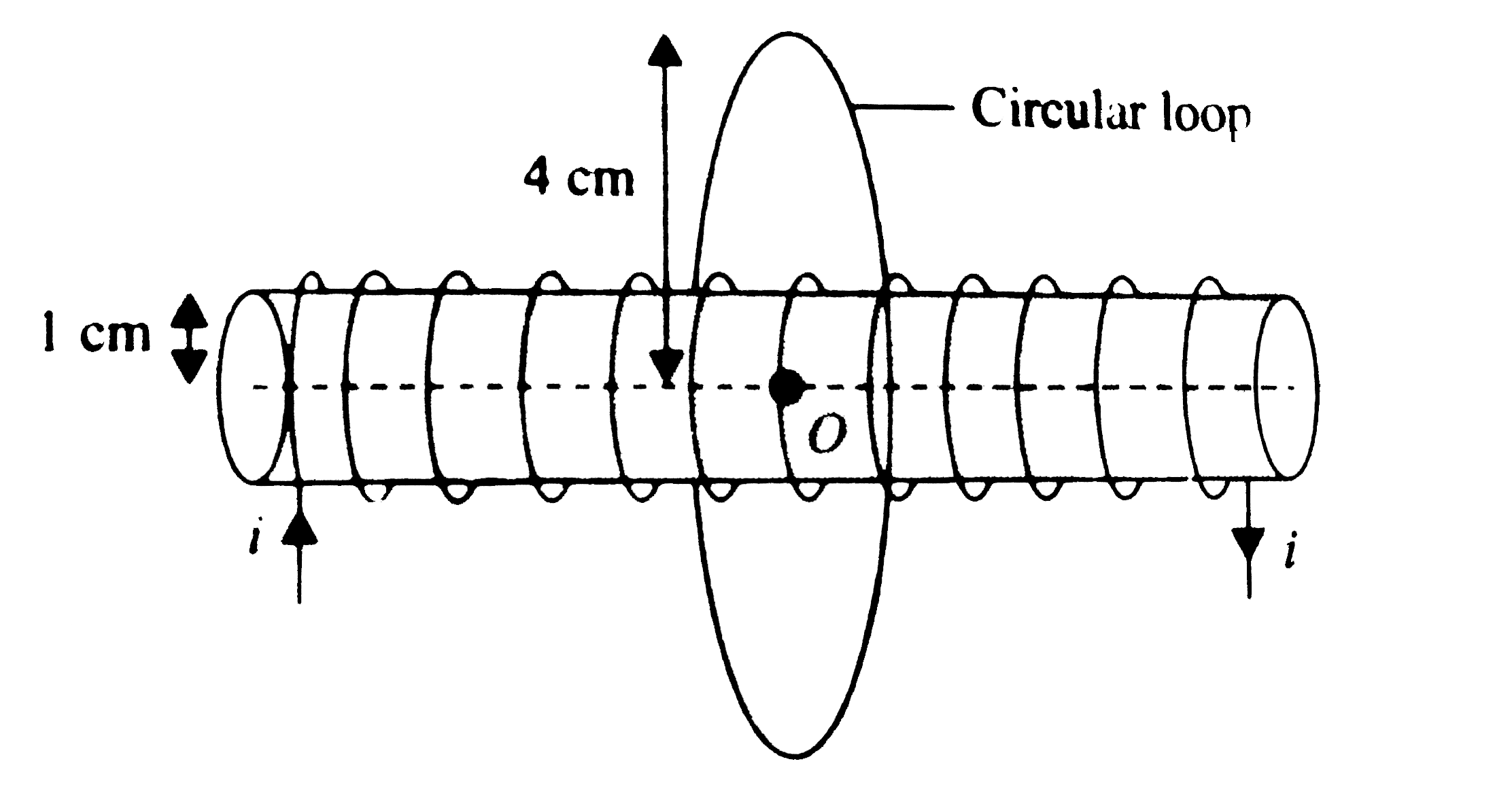
A current 't' in the solenoid results in magnetic field along its axis with magnitude B=(μ)ni at points well inside the solenoid on its axis. We can neglect the insignificant field outside the solenoid. This results in a magnetic flux (ϕ)B through the circular loop. If the current in the winding of solenoid is changed, it will also change the magnetic field B=(μ)0ni and hence also the magnetic flux through the circular loop. Obvisouly, it will result in an induced emf or induced electric field in the circular loop and an induced current will appear in the loop. Let current in the winding of solenoid be reduced at a rate of 75A/sec.
Magnetic of induced electric field strength in the circular loop is nearly We know that there is magnetic flux through the circular loop because of the magnetic field of current in the solenoid. For the purpose of circular loop, let us call it the external magnetic field. As current in the solenoid is reducing, external magnetic field for the circular loop also reduced resulting in induced current in the loop. Finally, as the solenoid current becomes zero, external field for the loop also becomes zero and stop changing. However, induced current in the loop will not stop at the instant at which the external field stops changing. This is because induced current itself produces a magnetic field that results in a flux through the loop. External field becoming zero without any further change will compel the induced current in the loop to become zero and so magnetic flux through the loop due to change in induced current will also change resulting in a further induced phenomenon that sustains currents in the loop even after the external field becomes zero.A4.7×10−7Vm−1B3.82×10−6Vm−1C2.3×10−5Vm−1DNone of these
A pair of parallel horizontal conducting rails of negligible resistance shorted at one end is fixed on a table. The distance between the rails is L. A conducting massless rod of resistance R can slide on the rails frictionlessly. The rod is tied to a massless string which passes over a pulley fixed to the edge of the table. A mass m tied to the other end of the string hangs vertically. A constant magnetic field B exists perpendicular to the table. If the system is released from rest, calculate

a. the terminal velocity achieved by the rod and
b. The acceleration of the mass of the instant when the velocity of the rod is half the terminal velocity.
View SolutionFigure shows a wire ab of length L and resistance R which can slide on a smooth pair of rails. Ig is current generator which supplies a constant current i in the circuit. If the wire ab slide at a speed v towards right, find the potential difference below a and b

(b) The current generator Ig show in the figure sends a constant current i through the circiut. The wire ab has a length L and mass m and can slide on the smooth horizontal rails connect to Ig . The entire system lies in a vertical magnetic field B . Find the velocity of the wire as a function of time.

(c) The system containing the rails and the wire of the previous part is kept vertically in a uniform horizontal magnetic field B that is perpendicular to the plane of the rails (figure). If is found that the wire stays in equilibrium. If th ewire ab is replaced by another wire of double its mass, how long will lit take in falling through a distance equal to its length?
The current generator Ig shown in figure sends a constant current i through the circuit. The wire cd is fixed and wire ab is made to slide on the smooth, thick rails with a constant velocity v toward right. Each of these wires has resistance r . Find the current through the wire cd .

View SolutionA small ball of mass m and charge q is attached to the bottom end of a piece of negligible mass thread of length l, whose top end is fixed. The system formed by the thread and ball is in vertical plane and is in uniform horizontal magnetic field B, which is perpendicular to the plane of figure and points into the paper

The ball is started with a velocity v0 from lower most point of circle in a direction perpendicular both to the magnetic induction and to direction of thread. The ball moves along a circular path such that thread remains tight during the whole motion. Neglect any loss of enery.
By what factor is the force acting on the thread (tension in thread) at point A is greater than at point C, when speed of the ball is the above stated one?
View SolutionOne electron gun is firing electrons with a speed V as shown in the figure. There is a target P which is to be hit. Electrons emerge from point 0 and line OP makes an angle with the direction of velocity of electrons. The length of OP is L.A uniform magnetic field B is applied parallel to line OP. Charge on the electron ise and the mass of electrons is m. What minimum magnetic field is needed so that electrons may hit the target P?
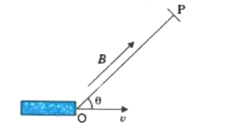
View SolutionFigure shows a situation similar to the previous problem. All parameters are the same except that a battery of emf ε and a variable resistance R are connected between O and C. The connecting wires have zero resistance. No external force is applied on the rod (except gravity, forces by the magnetic field and by the pivot).

In what way should the resistance R be changed so that the rod may rotate with uniform angular velocity in the clockwise direction? Express your answer in terms of the given quantities and the angle (θ) made by the rod OA with the horizontal.
View Solution