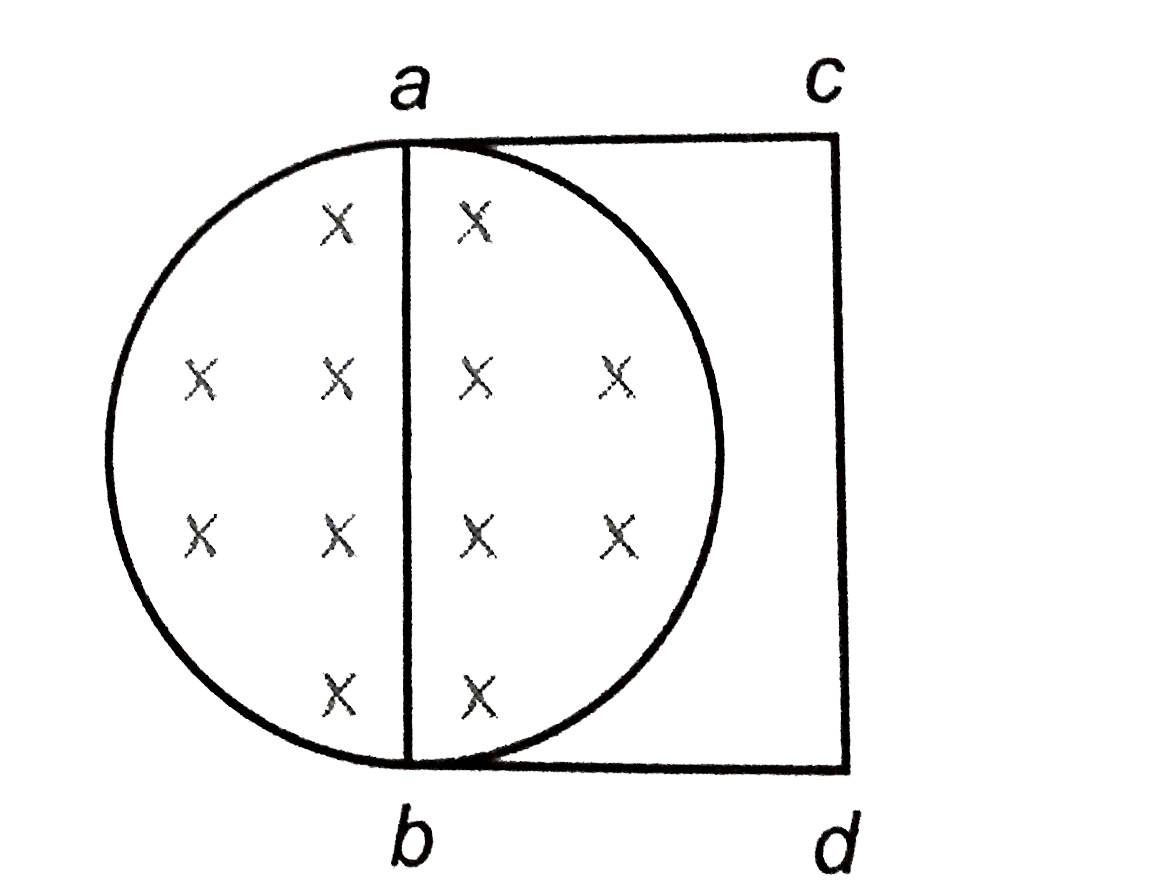
A uniform magnetic field B exists in a cylindrical region, shown dotted in. The magnetic field increases at a constant rate dBdt Consider a circle of radius r coaxial with the cylindrical region. (a) find the magnitude of the electric field E at a point on the circumference of the circle. (b) Consider a point P on the side of the square circumscribing the circle. Show that the component of the induced electric field at P along ba is the same as the magnitude found in part(a).

(a) work done per unit per unit test change is <br>phi.E.dl=e implies E phi .dl=(d phi)/(dt)implies E. 2 pi r =(dB)/(dt)xxA<br>implies E 2 pi r = pi r^2(dB)/(dt)<br>implies E= (pi r^2)/(2 pi r) (dB)/(dt) =(r/2)(dB)/(dt)<br>(b)whenthe□isconsred,
phi.e.dt=e<br>implies Exx2rxx4=(dB)/(dt)(2r)^2<br>implies E = (dB)/(dt) ((4r^2)/(8r)<br> impliesE=(r/2) (dB)/(dt). <br>(c) the electric field at the point has the same value as (a).
Topper's Solved these Questions
- ELECTROMAGNETIC INDUCTIONBOOK - HC VERMACHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - EXERCISE
9 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - HC VERMACHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Objective 2
10 Videos
- ELECTRIC FIELD AND POTENTIALBOOK - HC VERMACHAPTER - ELECTRIC FIELD AND POTENTIALEXERCISE - Exercises
75 Videos
- ELECTROMAGNETIC WAVESBOOK - HC VERMACHAPTER - ELECTROMAGNETIC WAVESEXERCISE - Exercises
9 Videos
Similar Questions
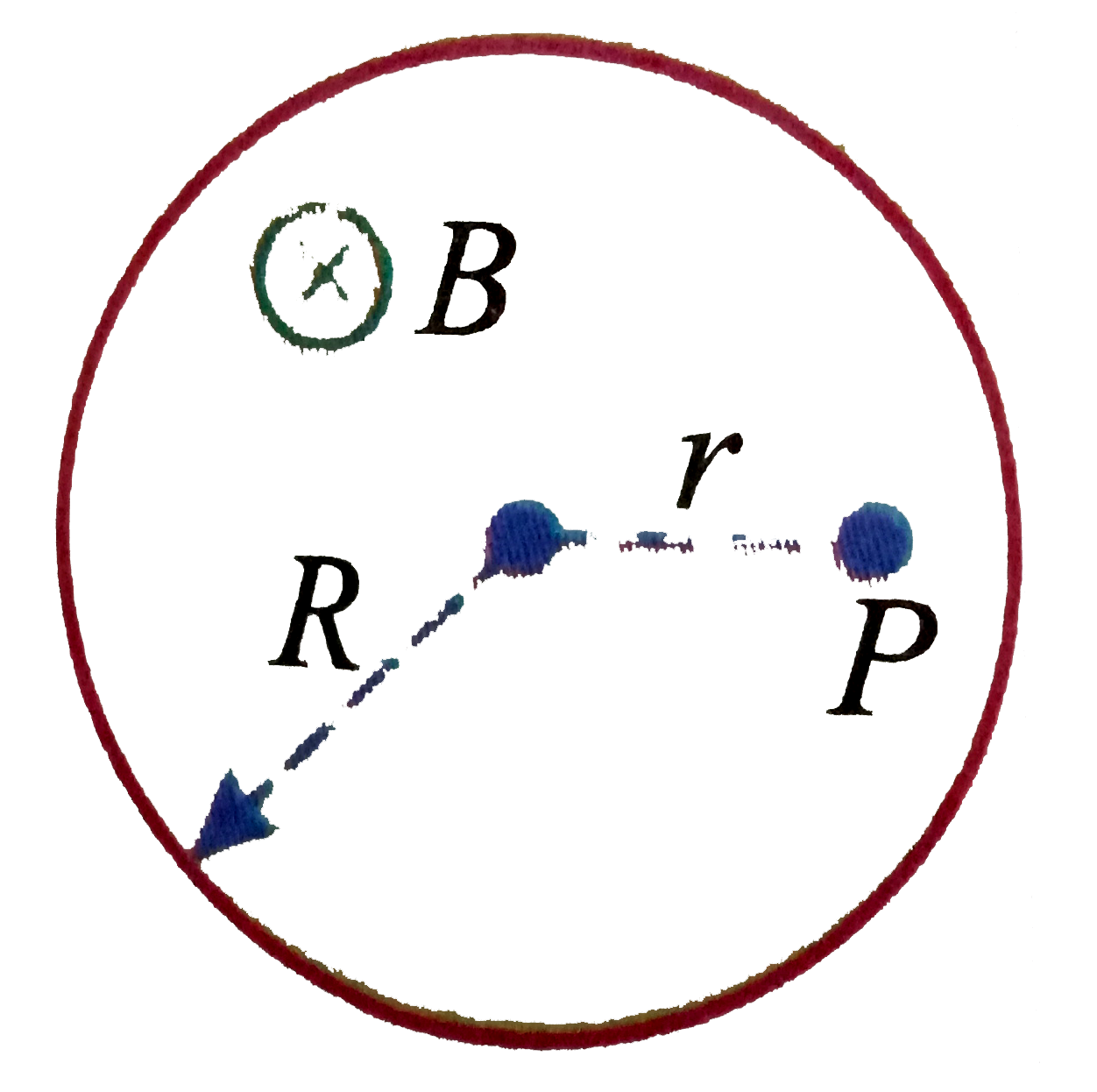
A uniform magentic field of induction B is confined in a cyclinderical region of radius R. If the field is incresing at a constant rate of dBdt=αT/s, then the intensity of the electric field induced at point P, distant r from the axis as shown in the figure is proportional to :
View SolutionA uniform but time varying magnetic field exists in cylindrical region and directed into the paper. If field decreases with time and a positive charge is placed at any point inside the region, then it moves :-

View Solution
Knowledge Check
A uniform magnetic field of induction B is confined to a cyclindrical region of radius R. The magnetic field is increasing at a constant rate of dB/dt (tesla/ second). A charge q of mass m, placed at the point P on the periphery of the fixed experiences an acceleration :
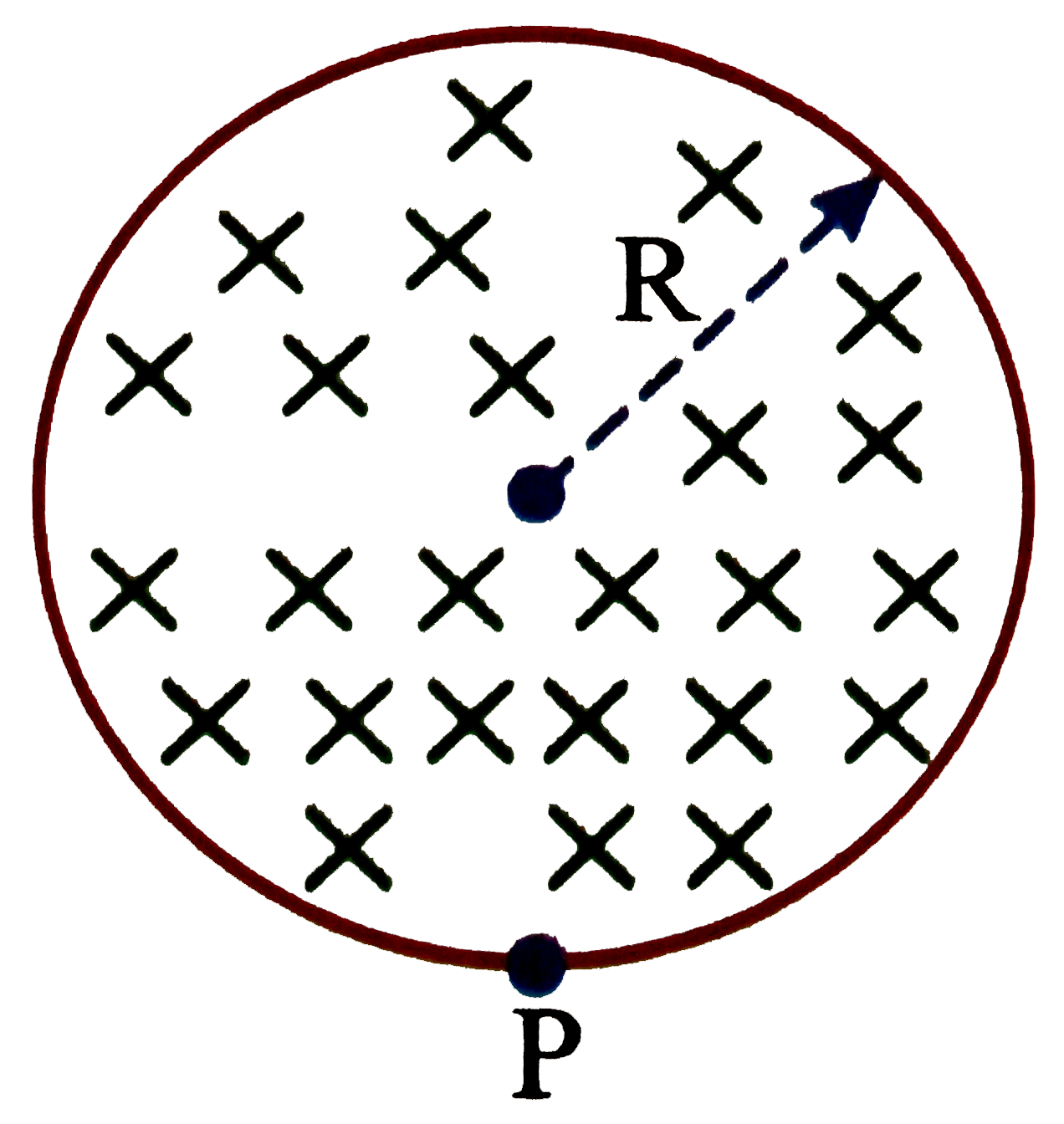 A12eRmdBdt towards leftB12eRmdBdt towards rightCeRmdBdt towards leftDzero
A12eRmdBdt towards leftB12eRmdBdt towards rightCeRmdBdt towards leftDzeroThe magnitude of electric field →E in the annular region of a charged cylindrical capacitor.
A(a) is same throughoutB(b) is higher near the outer cylinder than near the inner cylinderC(c) varies as 1/r, where r is the distance from axisD(d) varies as 1/r2 where r is the distance from the axis.A uniform magnetic field of induction B is confined to a cyclindrical region of radius R. The magnetic field is increasing at a constant rate of dB/dt (tesla/ second). A charge e of mass m, placed at the point P on the periphery of the fixed experiences an acceleration :
 A12eRmdBdt towards leftB12eRmeBdt towards rightCeRmdBdt towards leftDzero
A12eRmdBdt towards leftB12eRmeBdt towards rightCeRmdBdt towards leftDzero
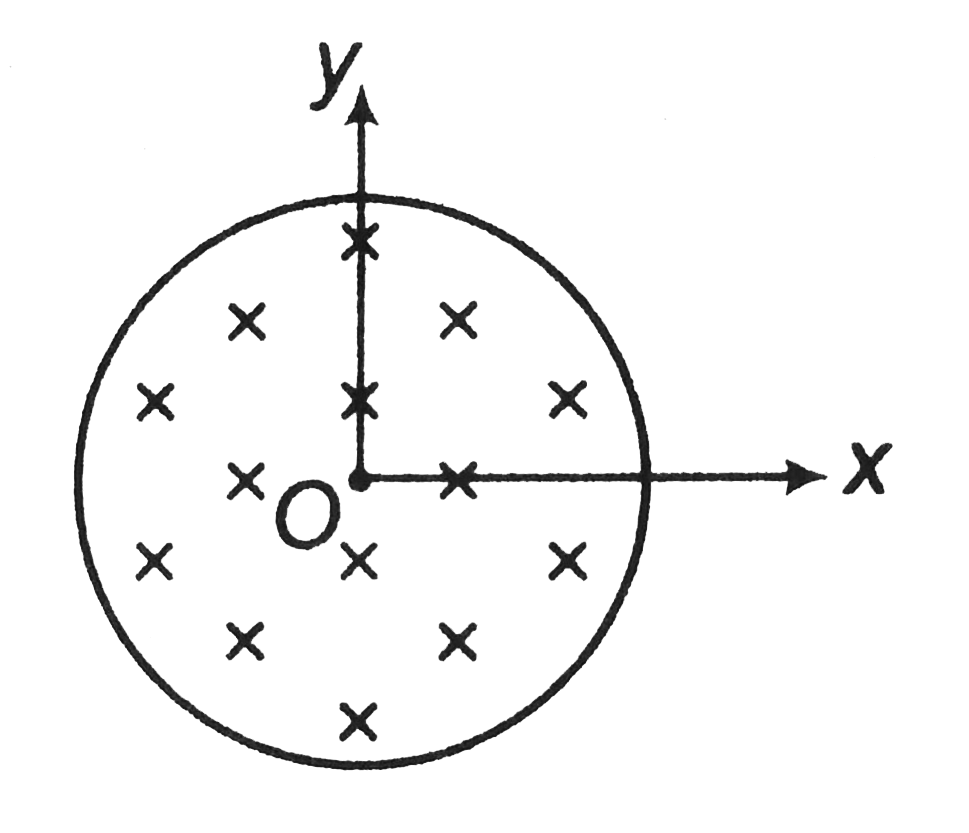
The magnetic field at all points within the cyllindrical region whose cross section is indicated in the accompanying Figure starts increasing at a constant rate α. T/s. find the magnitud of electric field as a function of r, the distance from the geometric centre of the region.

View SolutionMagnetic field in cylindrical region of radius R in inward direction is as shown in figure.
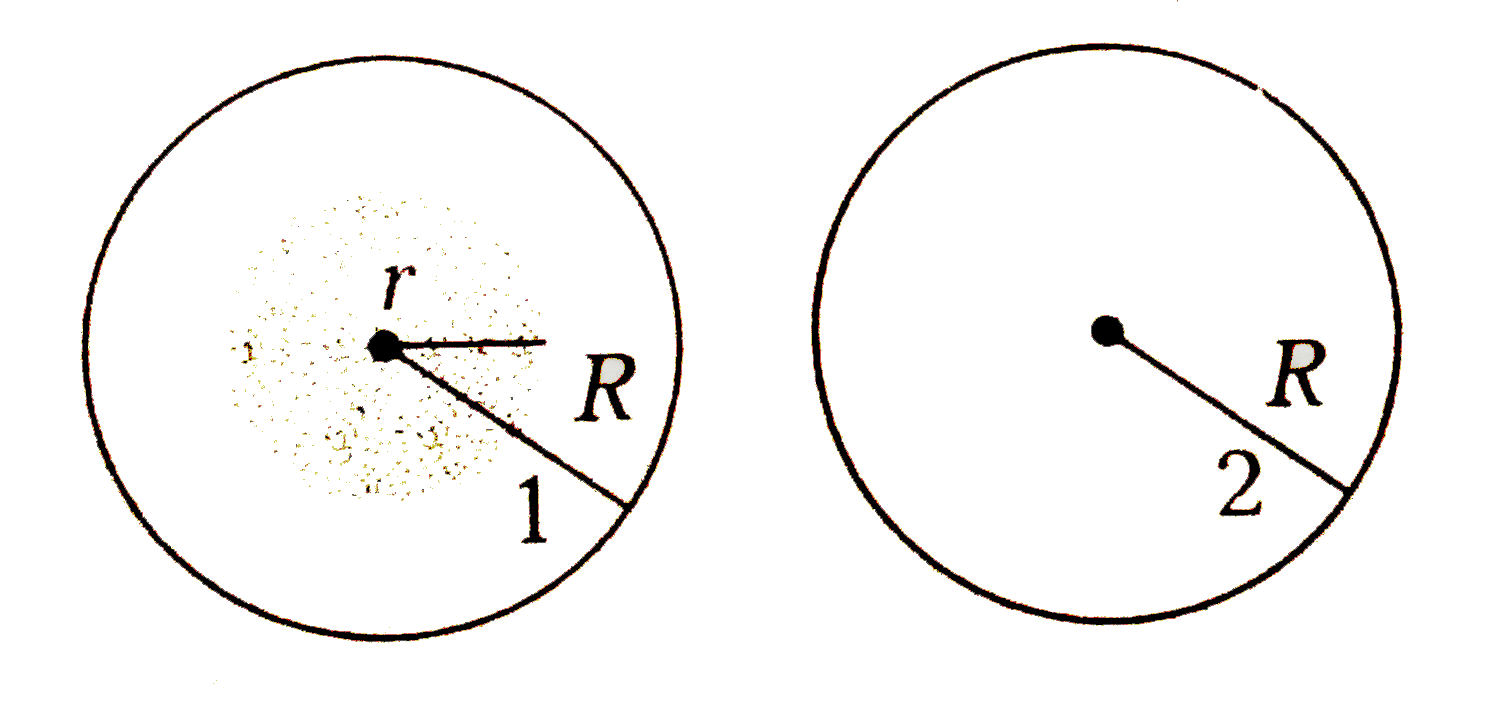
View SolutionA uniform magnetic field is restricted within a region of radius r. The magnetic field changes with time at a rate dBdt. Loop 1 of radius R > r encloses the region r and loop 2 of radius R is outside the region of magnetic field as shown in figure. Then, the emf generated is
View SolutionA uniform magnetic field B exists in a cylindrical region of radius I0cm as shown in figure. A uniform wire or length 80cm and resistance 44.0Ω is bent into a square frame and is placed with one side along a diameter of the cylindrical region. if the magnetic field increases at a constant rate of 0.0I0T/sec , the current induced in the frame
View SolutionA uniform but time varying magnetic field exists in cylindrical region and directed into the paper. If field decreases with time and a positive charge is placed at any point inside the region, then it moves :-

View Solution
