Unstable pions are produced as a beam in a nuclear reaction experiment . The pions leave the target at a speed of 0.995c. The intensity of the beam reduces to half its original value as the beam travels a distance of 39 m . Find the half - life of pions (a) in the laboratory frame, (b) in their rest frame.
(a) The intensity of the pion beam reduces to half its original value in one half - life. The half - life of the pions as measured in the laboratory is
t12=39m0995c=39m0.995×3×108ms−1
=1.3×10−7. (b) The events - a pion leaving the target and its decaying - occur at the same place in the pion - frame . thus, the time measured in the pion - frame is the proper time and is the smallest. It is equal to
t'12=t12(√1−v2c2)=(1.3×10−7s)(√1−(0.995)2
=1.3×10−8s.
Topper's Solved these Questions
- THE SPECIAL THEORY OF RELATIVITYBOOK - HC VERMACHAPTER - THE SPECIAL THEORY OF RELATIVITYEXERCISE - Objective
7 Videos
- THE SPECIAL THEORY OF RELATIVITYBOOK - HC VERMACHAPTER - THE SPECIAL THEORY OF RELATIVITYEXERCISE - Objective 2
6 Videos
- THE SPECIAL THEORY OF RELATIVITYBOOK - HC VERMACHAPTER - THE SPECIAL THEORY OF RELATIVITYEXERCISE - Exercise
1 Videos
- THE NUCLEOUSBOOK - HC VERMACHAPTER - THE NUCLEOUSEXERCISE - Exercises
53 Videos
- THERMAL AND CHEMICAL EFFECT OF ELECTRIC CURRENTBOOK - HC VERMACHAPTER - THERMAL AND CHEMICAL EFFECT OF ELECTRIC CURRENTEXERCISE - Exercises
24 Videos
Similar Questions
What will be the distance a pion (pi-meson) travels before it decays, if its speed is v - 0.99c and its intrinsic lifetime is to = 2.6×10−8 s? What would be the transit distance if there is no relativistic time dilation? The distance is measured in the laboratory reference frame.
View SolutionAn accelration produces a narrow beam of protons, each having an initial speed of v0. The beam is directed towards an initially uncharges distant metal sphere of radius R and centered at point O. The initial path of the beam is parallel to the axis of the sphere at a distance of (R/2) from the axis, as indicated in the diagram.

The protons in the beam that collide with the sphere will cause it to becomes charged. The subsequentpotential field at the accelerator due to the sphere can be neglected. The angular momentum of a particle is defined in a similar way to the moment of a force. It is defined as the moment of its linear momentum, linear replacing the force. We may assume the angular momentum of a proton about point O to be conserved. Assume the mass of the proton as mP and the charge on it as e. Given that the potential of the sphere increases with time and eventually reaches a constant velue.
After a long time, when the potential of the sphere reaches a constant value, the trajectory of proton is correctly sketched as

View Solution
Knowledge Check
An accelration produces a narrow beam of protons, each having an initial speed of v0. The beam is directed towards an initially uncharges distant metal sphere of radius R and centered at point O. The initial path of the beam is parallel to the axis of the sphere at a distance of (R/2) from the axis, as indicated in the diagram.
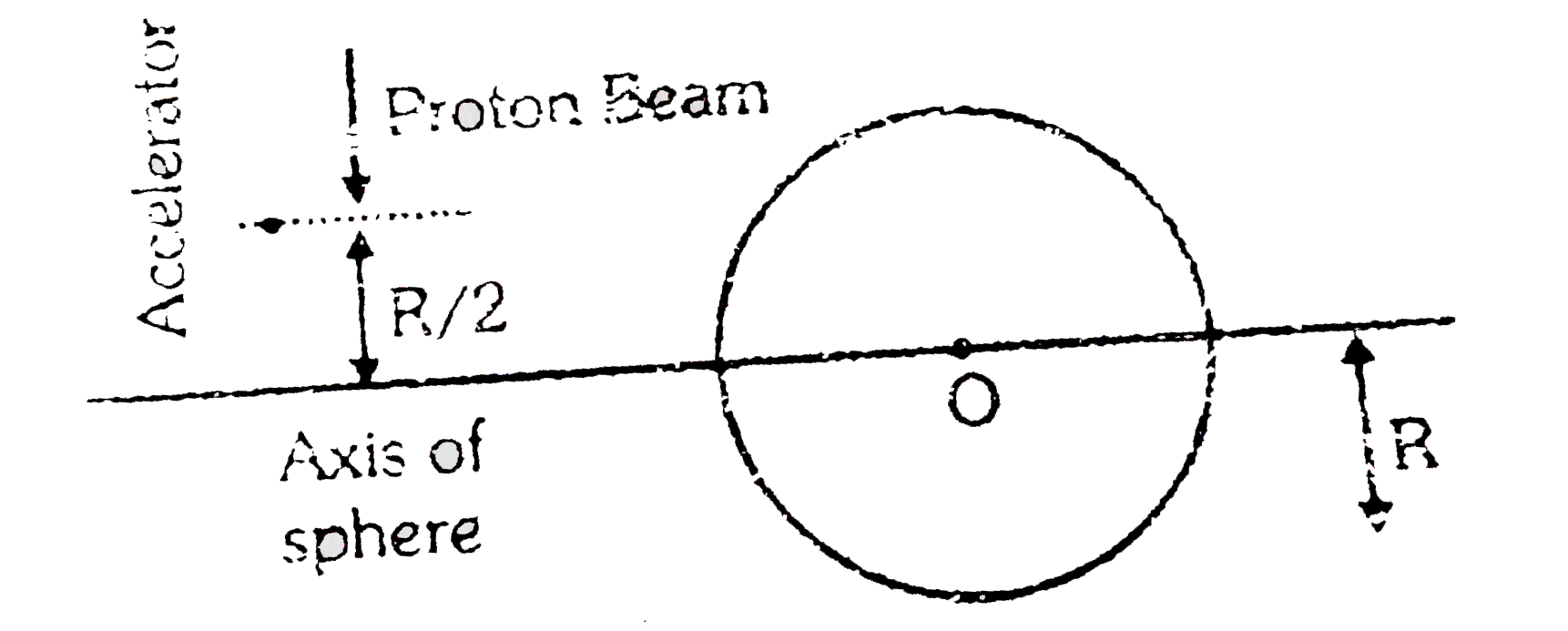
The protons in the beam that collide with the sphere will cause it to becomes charged. The subsequentpotential field at the accelerator due to the sphere can be neglected. The angular momentum of a particle is defined in a similar way to the moment of a force. It is defined as the moment of its linear momentum, linear replacing the force. We may assume the angular momentum of a proton about point O to be conserved. Assume the mass of the proton as mP and the charge on it as e. Given that the potential of the sphere increases with time and eventually reaches a constant velue.
One the potential of the sphere has reached its final, constant value, the minimum speed v of a proton along its trajectory path is given byAv0Bv0/2C2v0DNone of theseAn accelration produces a narrow beam of protons, each having an initial speed of v0. The beam is directed towards an initially uncharges distant metal sphere of radius R and centered at point O. The initial path of the beam is parallel to the axis of the sphere at a distance of (R/2) from the axis, as indicated in the diagram.

The protons in the beam that collide with the sphere will cause it to becomes charged. The subsequentpotential field at the accelerator due to the sphere can be neglected. The angular momentum of a particle is defined in a similar way to the moment of a force. It is defined as the moment of its linear momentum, linear replacing the force. We may assume the angular momentum of a proton about point O to be conserved. Assume the mass of the proton as mP and the charge on it as e. Given that the potential of the sphere increases with time and eventually reaches a constant velue.
After a long time, when the potential of the sphere reaches a constant value, the trajectory of proton is correctly sketched as
 A1B2C3D4
A1B2C3D4An accelration produces a narrow beam of protons, each having an initial speed of v0. The beam is directed towards an initially uncharges distant metal sphere of radius R and centered at point O. The initial path of the beam is parallel to the axis of the sphere at a distance of (R/2) from the axis, as indicated in the diagram.

The protons in the beam that collide with the sphere will cause it to becomes charged. The subsequentpotential field at the accelerator due to the sphere can be neglected. The angular momentum of a particle is defined in a similar way to the moment of a force. It is defined as the moment of its linear momentum, linear replacing the force. We may assume the angular momentum of a proton about point O to be conserved. Assume the mass of the proton as mP and the charge on it as e. Given that the potential of the sphere increases with time and eventually reaches a constant velue.
The total energy (E) of a proton in the beam travelling with seed v at a distance of r(r≥R) from point O. Assuming that the sphere has acquired an electrostatic charge Q isAeQ4πε0rBless than eQ4πε0rCgreater than eQ4πε0rDzero
An accelration produces a narrow beam of protons, each having an initial speed of v0. The beam is directed towards an initially uncharges distant metal sphere of radius R and centered at point O. The initial path of the beam is parallel to the axis of the sphere at a distance of (R/2) from the axis, as indicated in the diagram.

The protons in the beam that collide with the sphere will cause it to becomes charged. The subsequentpotential field at the accelerator due to the sphere can be neglected. The angular momentum of a particle is defined in a similar way to the moment of a force. It is defined as the moment of its linear momentum, linear replacing the force. We may assume the angular momentum of a proton about point O to be conserved. Assume the mass of the proton as mP and the charge on it as e. Given that the potential of the sphere increases with time and eventually reaches a constant velue.
The total energy (E) of a proton in the beam travelling with seed v at a distance of r(r≥R) from point O. Assuming that the sphere has acquired an electrostatic charge Q is
View SolutionThere is a narrow beam of negative pions with kinetic energy T equal to the rest energy of these particles. Find the ratio of fluxes at the sections of the beam separated by a distance l=20m. The proper mean lifetime of these poins is τ0=25.5ns.
View Solution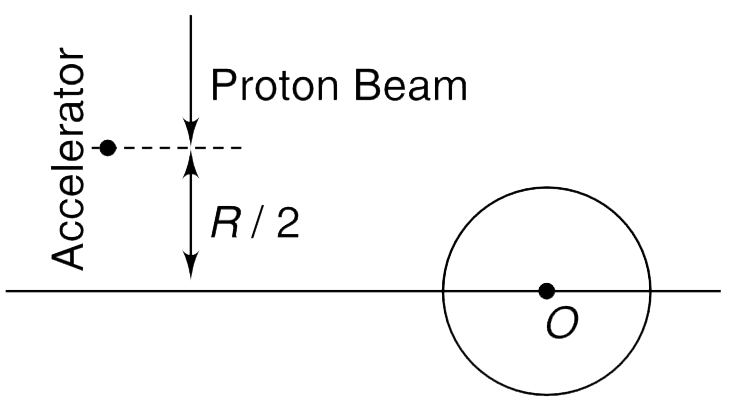
A proton accelerator produces a narrow beam of protons, each having an initial speed of v0. The beam is directed towards an initially uncharged distant metal sphere of radius R. The sphere is fixed and centered at point O. The initial path of the beam is at a distance of (R/2) from the centre, as indicated in the diagram. The protons in the beam that collide with the sphere get absorbed and cause it to become uniformly charged. The subsequent potential field at the accelerator due to the sphere can be neglected. Assume the mass of the proton as mP and the charge on it as e.
(a) After a long time, when the potential of the sphere reaches a constant value, sketch the trajectory of proton in the beam. (b) Once the potential of the sphere has reached its final, constant value, find the minimum speed v of a proton along its trajectory path. (c) Find the limiting electric potential of the sphere.
View SolutionThe yeild of a nuclear reaction producing radionuclides may be described in two ways: either by the ratio ω of the numbers of nuclear reactions to the number of bombarding particles, or by the quantity k, the ratio of the activity of the formed radionuclide to the number of bombarding particles, Find:
(a) the half-life of the formed radionuclide, assuming ω and k to be known:
(b) the yield ω of the reaction Li7(p,n)Be7 if after irradiation of a lithum target by a beam or protons(over t=2.0) hours and with =1.35.108dis/s and its half-life to T=53days.
View SolutionTwo strange particles A and B in space, exert no force on each other when they are at a separation greater than x0=1.0 m. When they are at a distance less than x0, they repel one another along the line joining them. The repulsion force is constant and does not depend on the distance between the particles. This repulsive force produces an acceleration of 6ms–2 in A and 2ms–2 in B when the particles are at separation less than x0. In one experiment particle B is projected towards A with a velocity of 2ms–1 from a large distance so as to hit A head on. The particle A is originally at rest and the system of two particles do not experience any external force.
(a) Find the ratio of mass of A to that of B.
(b) Find the minimum distance between the particles during subsequent motion. (c) Find the final velocity of the two particles.
View Solution
