Two events A and B occur at places separated by 106km, B occuring 5s after A . (a) Find the velocity of a frame in which these events occur at the same place . (b)What is the time interval between the events in this frame ?

(a) Suppose the events A and B occur at points X and Y at times t_A and t_B where t_B = t_A +5 s. Consider a small train which is at the point X when the event A occurs. Suppose, this same train moves towards Y and reaches the point Y when the events A and B occur at the same place in the train frame . This frame moves 106 km in 5s as seen from the original frame . Thus, the velocity of the train frame is
v=106km5s=2×10sms−1
(b) As the events A and B occur at the same place in the train frame, the time interval between the events measured in this frame is the proper interval . Thus , this time interval is ,
=(55)(√1−v2c2)=(5s)(√1−(23)2
=3.7s
Topper's Solved these Questions
- THE SPECIAL THEORY OF RELATIVITYBOOK - HC VERMACHAPTER - THE SPECIAL THEORY OF RELATIVITYEXERCISE - Objective
7 Videos
- THE SPECIAL THEORY OF RELATIVITYBOOK - HC VERMACHAPTER - THE SPECIAL THEORY OF RELATIVITYEXERCISE - Objective 2
6 Videos
- THE SPECIAL THEORY OF RELATIVITYBOOK - HC VERMACHAPTER - THE SPECIAL THEORY OF RELATIVITYEXERCISE - Exercise
1 Videos
- THE NUCLEOUSBOOK - HC VERMACHAPTER - THE NUCLEOUSEXERCISE - Exercises
53 Videos
- THERMAL AND CHEMICAL EFFECT OF ELECTRIC CURRENTBOOK - HC VERMACHAPTER - THERMAL AND CHEMICAL EFFECT OF ELECTRIC CURRENTEXERCISE - Exercises
24 Videos
Similar Questions
Knowledge Check
Two events occur on the x axis separated in time by Δt and in space by Δx. A reference frame, traveling at less than the speed of light, in which the two events occur at the same time
AExists no matter what the values of Δx and ΔtBExists only if Δx/Δt<cCExists only if Δx/Δt>cDDoes not exist under any conditionIf P(A) and P(B) are the probabilities of occurrence of two events A and B, then the probability that exactly one of the two events occur, is
AP(A∪¯¯¯B)+P(¯¯¯A∩B)BP(A∪B)−P(A∩B)CP(A) + P(B)DP(A)+P(B)−2P(A∩B)If A, B, C are three events, then what is the probability that at least two of these events occur together?
AP(A∩B)+P(B∩C)+P(C∩A)BP(A∩B)+P(B∩C)+P(C∩A)−P(A∩B∩C)CP(A∩B)+P(B∩C)+P(C∩A)−2P(A∩B∩C)DP(A∩B)+P(B∩C)+P(C∩A)−3P(A∩B∩C)
At two points of an inertial reference frame separated by a distance along the x-axis of l=x2−x1 two events take place slmultaneously. Find the time interval between the events in an !arbitrary inertial reference frame.
View SolutionThe space-time diagram, shows three events A, B, and C which occurred on the x axis of some inertial reference frame. Find:
(a) the time interval between the events A and B in the reference frame where the two events occurred at the same point,
(b) the distance between the points at which the events A and C occured in the reference frame where these two events are simultaneous.
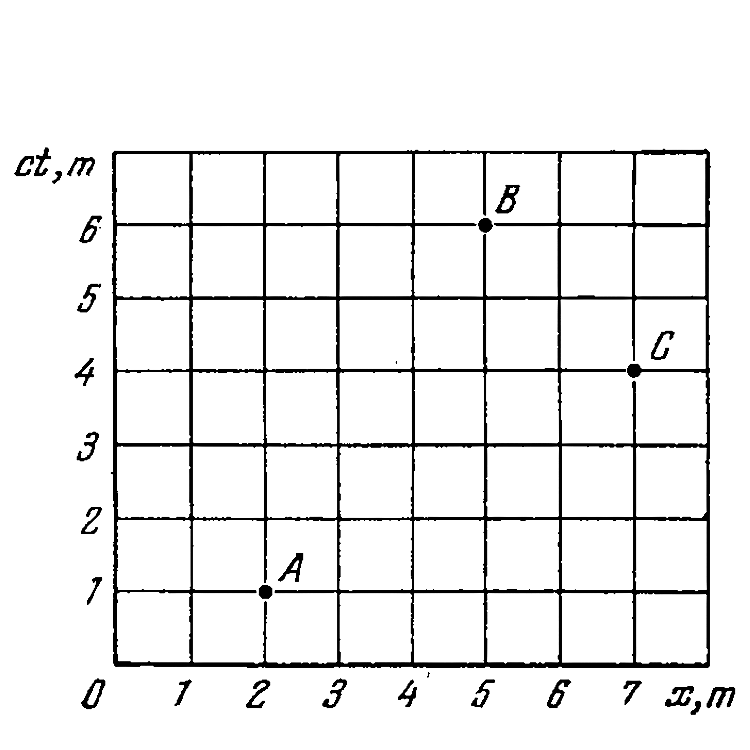
View SolutionAt two points of the reference frame K two events occurred separated by a time interval Δt. Demonstrate that if these events obey the cause-and-effect relationship in the frame K (e.g. a shot fired and a bullet hitting a target), they obey that relationship in any other inertial reference frame K′.
View SolutionTwo events A and B are such that P(B) = 0 . 55 and P(AB') = 0 . 15 . The probability of occurence of at least one of event is
View SolutionIf A. B. C are three events, then what is the probability that atleast two of these events occur together?
View Solution
