Instantaneous Velocity
Step by step video & image solution for Instantaneous Velocity by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Similar Questions
The position of a particle moving along the x axis is given in centimeters by x=9.75+1.50t3, where t is in seconds. Calculate (a) the average velocity during the time interval t=2.00s to t=3.00s, (b) the instantaneous velocity at t=2.00s , (c) the instantaneous velocity at t=3.00s, (d) the instantaneous velocity at t=2.50s, and (e) the instantaneous velocity when the particle is midway between its positions at t=2.00s and t=3.00s . (f) Graph x versus t and indicate your answers graphically
View Solution_S01_033_Q01.png)
In a typical young's double slit experiment a point source of monochromatic light is kept as shown in the figure. If the source is given an instantaneous velocity v=1 mm per second towards the screen, then the instantaneous velocity of central maxima is given as α×10−βcm/s upward in scientific notation find the value of α+βView Solution
Knowledge Check
- Question 1 - Select One
Which of the following statements is /are correct ?
I.Average speed over a finite interval of times is greater or equal to the magnitude of the average velocity.
The instantaneous speed at an instant is equal to the magnitude of the instantaneous velocity at that instant.AOnly IBOnly IICBoth I and IIDNone is correct - Question 2 - Select One
A particle moving in the positive x-direction has initial velocity v0. The particle undergoes retardation kv2 , where vis its instantaneous velocity. The velocity of the particle as a function of time is given by:
Av=v0/(1+kv0t)Bv=2v01+ktCv=v0ktDv=v0(1+k2v02t) - Question 3 - Select One
A particle moving in the positive x-direction has initial velocity v0. The particle undergoes retardation kv2 , where vis its instantaneous velocity. The velocity of the particle as a function of time is given by:
Av=v0/(1+kv0t)Bv=2v01+ktCv=v0ktDv=v0(1+k2v20t)
How can we measure the instantaneously velocity graphically?
View SolutionThe instantaneous velocities of two particles of masses 200 g and 400 g at a given time are 12ˆi−7ˆj−5ˆk m/s and 8ˆi−9ˆj−5ˆk m/s, respectively. Calculate the instantaneous velocity of the centre of mass of the system.
View SolutionA particel moving along a straigh line has instantaneous velocities during the first 5 seconds as given below. Draw a velocity - time graph
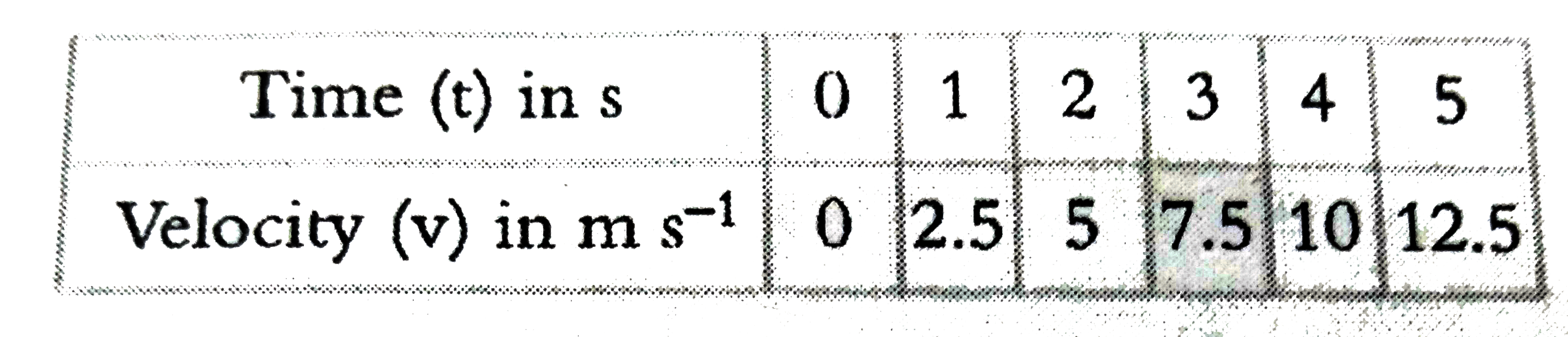
View SolutionReferring to the previous illustration
(a) What is the significance of positive and negative values of instantaneous velocities?
(b) What are the distance covered and displacement during t= 2 sec?View SolutionAssertion : The average and instantaneous velocities have same value in a uniform motion.
Reason : In uniform motion, the velocity of an object increases uniformlyView Solution