Theorem 10.12 : If the sum of a pair of opposite angles of a quadrilateral is 180º, the quadrilateral is cyclic.

Video Solution

Text Solution

Verified by Experts

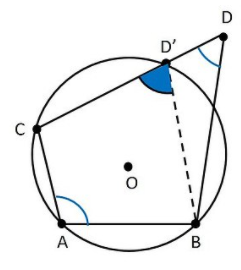
Since $A$ , $B$ , $C$ are non-collinear, on circle passes through them. Let us draw a circle with center $O$ .
Let us assume $D$ does not lie on circle.
$A B C D'$ is a cyclic quadrilateral.
$∠ B A C \frac{+}{B} D' C = 180$
But, given that, $∠ B A C + ∠ B D C = 180$
Thus,
$∠ B D' C = ∠ B D C$
This is only true when $D$ and $D'$ coincides.
Point $D$ lies on circle and $A B C D$ is cyclic quadrilateral.

Updated on:21/07/2023