The sum of either pair of opposite angles of a cyclic quadrilateral is 1800 OR The opposite angles of a cyclic quadrilateral are supplementary.
Video Solution
Text Solution
TO prove=∠A+∠C=180∘,∠B+∠DD=180∘
Chord AB∠ACB=∠ADB−(1)
Chord BC∠BAC=∠BDC−(2)
adding equation 1 and 2
∠ACB+∠BAC=∠ADB+∠BDC
∠ACB+∠BAC+∠ABC=∠ADC+∠ABC
∠D+∠B=180∘
∠B+∠D=180∘
∠A+∠B+∠C+∠D=360∘
∠A+∠C+180∘=360∘=180∘
∠B+∠D=180∘.
|
Topper's Solved these Questions
Similar Questions
Knowledge Check
If an exterior angle of a cyclic quadrilateral be 50∘, then the opposite interior angle is :
A130∘B40∘C50∘D90∘The quadrilateral formed by the bisectors of the angles of a parallelogram is a
 ArectangleBsquareCparallelogramDcyclic quadrilateral
ArectangleBsquareCparallelogramDcyclic quadrilateral
Theorem 10.11 : The sum of either pair of opposite angles of a cyclic quadrilateral is 180º.
View SolutionProve that the sum of opposite pair of angles of a cyclic quadrilateral is 180∘
View SolutionDefinition of Cyclic quadrilateral
View SolutionABCD is a cyclic quadrilateral (see Figure). Find the angles of the cyclic quadrilateral.
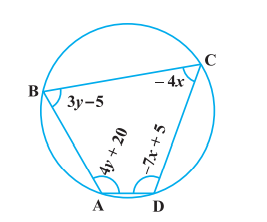
View SolutionIf the sum of any pair of opposite angles of a quadrilateral is 180∘; then the quadrilateral is cyclic.
View SolutionTheorem 10.12 : If the sum of a pair of opposite angles of a quadrilateral is 180º, the quadrilateral is cyclic.
View Solution
