Consider the following in respect of two events A and B : 1. P(A occurs but not B ) =P(A)−P(B) if B⊂A. 2. P(A alone or B alone occurs)=P(A)+P(B)−P(A∩B). 3. P(A∪B)=P(A)+P(B) if A and B are mutually exclusive . Which of the above is/are correct?
A
1 only
B
1 and 3 only
C
2 and 3 only
D
1 and 2 only
Video Solution
Text Solution
The correct Answer is:B
Statement 1 : If B⊂A, then
P(A−B)=P(A)−P(A∩B) .
=P(A)−P(B)
∴ It is correct.
Statement 2 , P(A alone or B alone).
P(A)−P(A∩B)+P(B)−P(A∩B)
=P(A)+P(B)−2P(−A∩B).
∴ It is false .
Statement 3: If A, B are mutually exclusive events , then P(A∩B)=0
⇒P(A∩B)=0.
⇒P(A∩B)=P(A)+P(B).
It is correct.
|
Topper's Solved these Questions
- POLYNOMIAL,QUADRATIC EQUATION & INEQUALITIESBOOK - NDA PREVIOUS YEARSCHAPTER - POLYNOMIAL,QUADRATIC EQUATION & INEQUALITIESEXERCISE - Math
170 Videos
- PROPERTIES OF TRIANGLE, INVERSE TRIGONOMETRIC FUNCTIONBOOK - NDA PREVIOUS YEARSCHAPTER - PROPERTIES OF TRIANGLE, INVERSE TRIGONOMETRIC FUNCTIONEXERCISE - MCQ
103 Videos
Similar Questions
Knowledge Check
Consider the following in respect of two events A and B.
I. P(A occurs but not B) = P(A) - P(B) if C⊂A
II.P(A alone or B alone occurs) = P(A) + P(B) - P(A∩B)
III P(A uu B) = P(A) + P(B) if A and B are mutually exclusive.
Which of the above is/are correct?A1 onlyBI and III onlyC2 and 3 onlyD1 and 2 onlyIf A and B are two mutually exclusive events, then
AP(A)<P(¯¯¯B)BP(A)>P(¯¯¯B)CP(A)<P(B)DNone of theseConsider the following statements : For any two sets A and B
(1)(A-B) ∪B=A
(2) (A-B)∪ A=A
(3) (A-B) ∩B=ϕ
(4) A⊆B⇒A∪B=B of these statements:A(A−B)∪B=AB(A−B)∪A=AC(A−B)nB=ϕDA⊆B⇒A∪B=B
Consider the following reaction sequence
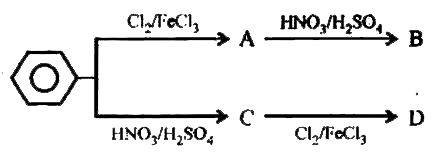
In this B and D respectively are
View SolutionIf A and B are two events, then which one of the following is/are always true?
View SolutionFor two given events A and B P(A∩B)=
View SolutionFor any two events A and B in a sample space
View SolutionConsider of the following sequence of reaction
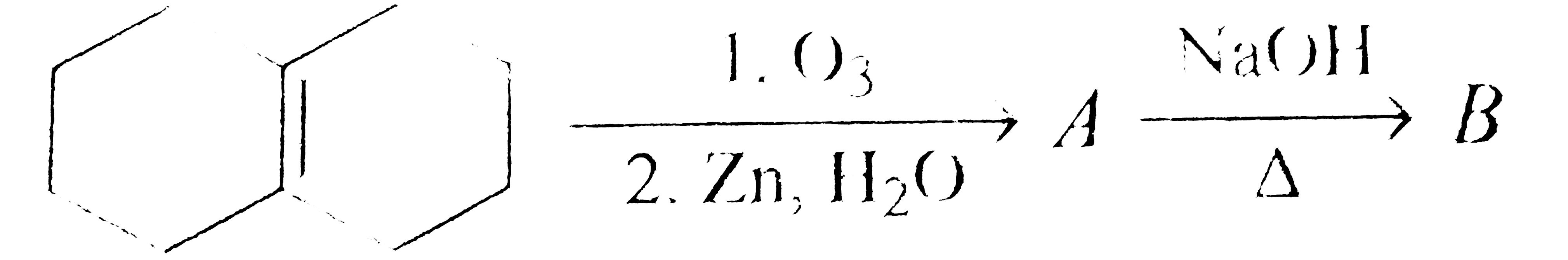
Product A and B respectively :
View Solution
