Let ABCD be a p[arallelogram whose diagonals intersect at P and let O be the origin. Then prove that →OA+→OB+→OC+→OD=4→OP.
−−→OP
2−−→OP
3−−→OP
4−−→OP
The correct Answer is:D
Diagonals of a parallelogram bisect each other. Therefore, P is the mid point of AC and BD both.
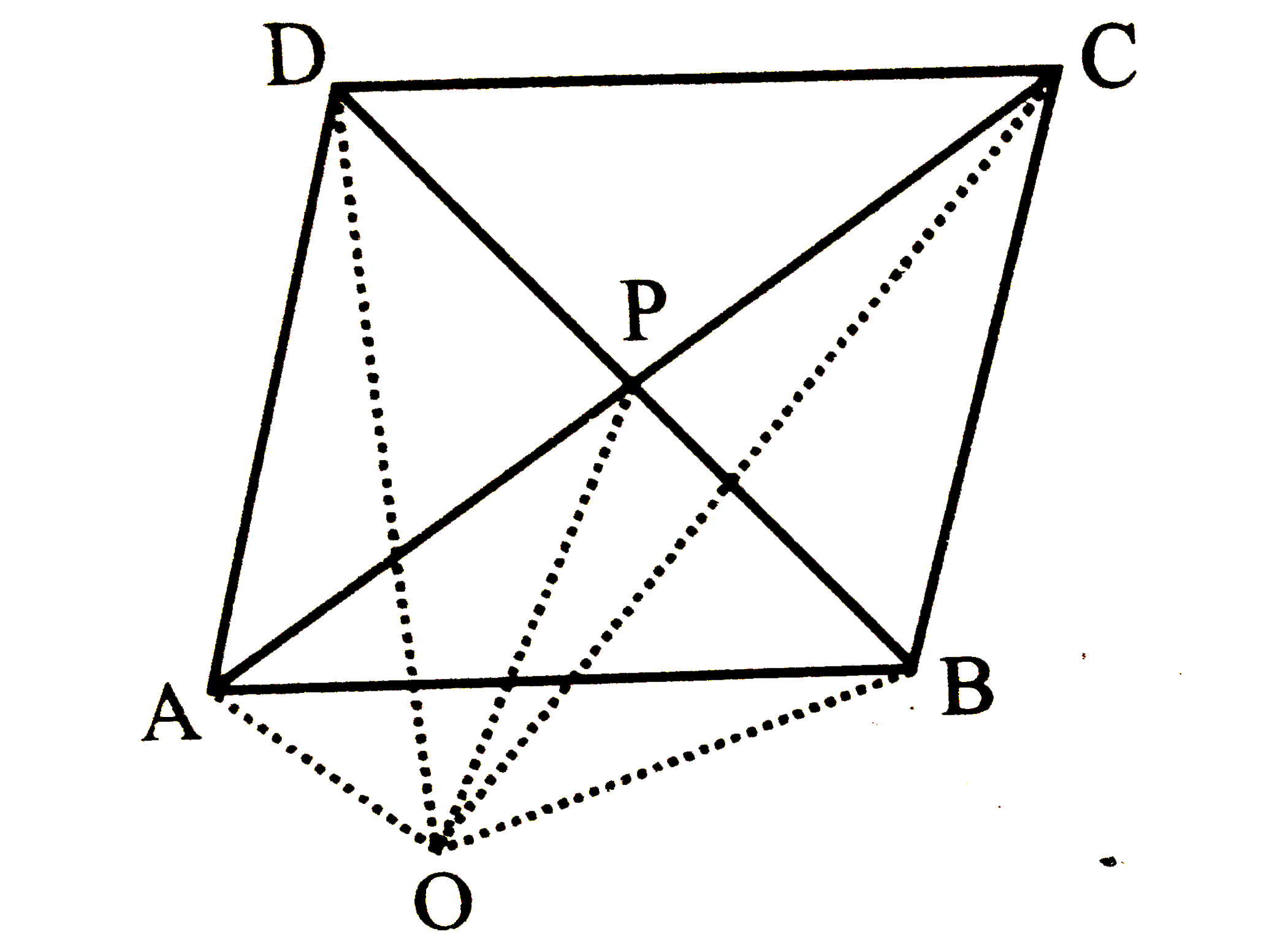
So, in ΔOAC,−−→OA+−−→OC=2−−→OP
and in ΔODB,−−→OB+−−→OD=2−−→OP
⇒−−→OA+−−→OC=2−−→OPand−−→OB+−−→OD=2−−→OP
⇒−−→OA+−−→OB+−−→OC+−−→OD=4−−→OP
Topper's Solved these Questions
Similar Questions
Knowledge Check
Let ABCD be a parallelogram whose diagonals intersect at P and let O be the origin. What is −−→OA+−−→OB+−−→OC+−−→OD equal to
A2−−→OPB4−−→OPC6−−→OPD8−−→OP
ABCD is parallelogram and P is the point of intersection of its diagonals. If O is the origin of reference, show that →OA+→OB+→OC+→OD=4→OP.
View SolutionABCD is a parallelogram whose diagonals intersect at O. If P is any point on BO, prove that: ar (ADO)=AR (CDO) ar ( ABP)= ar ( CBP)
View SolutionIf O is a point in space, ABC is a triangle and D,E,F are the mid-points of the sides BC,CA and AB respectively of the triangle, prove that →OA + →OB+→OC=→OD+→OE+→OF.
View SolutionIf →a+→b+→c=o, prove that →a×→b=→b×→c=→c×→a
View SolutionIf O is the circumcentre, G is the centroid and O' is orthocentre or triangle ABC then prove that: −−→OA+−−→OB+−−→OC=−−−→OO'
View SolutionIf O is the circumcentre and P the orthocentre of ΔABC, prove that −−→OA+−−→OB+−−→OC=−−→OP.
View SolutionA,B,CandD are any four points in the space, then prove that ∣∣→AB×→CD+→BC×→AD+→CA×→BD∣∣=4 (area of ABC .)
View Solution
