A variable plane passes through a fixed point (a,b,c) and cuts the coordinate axes at points A,B,andC. Show that eh locus of the centre of the sphere OABCisax+by+cz=2.
xa+yb+zc=1
ax+by+cz=1
ax+by+cz=2
xa+yb+zc=2
The correct Answer is:C
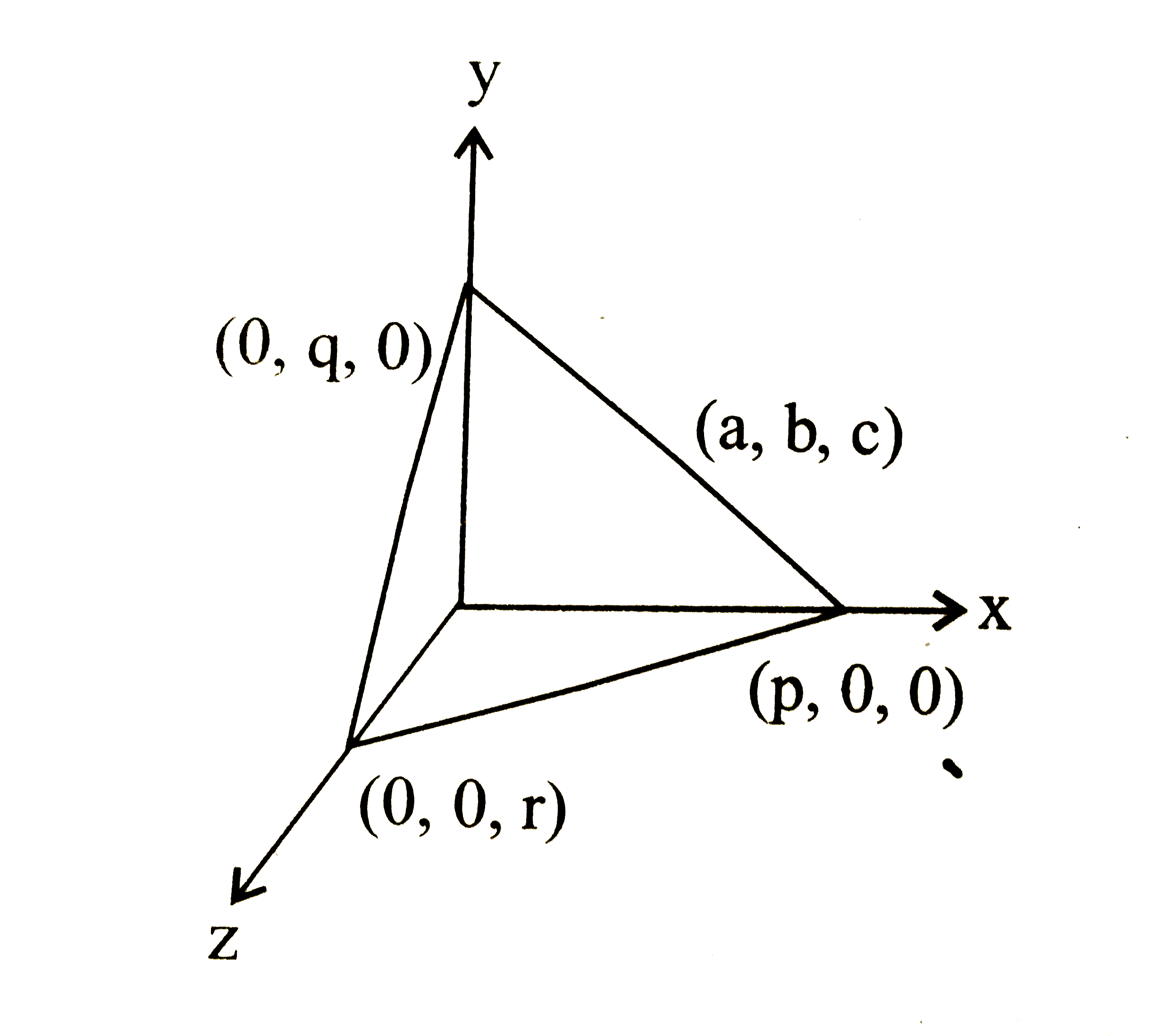 Equation of plane passing through points (p,0,0),(0,q,0) and (0,0,r) and (0,0,r) is xp+yq+zr=1
Equation of plane passing through points (p,0,0),(0,q,0) and (0,0,r) and (0,0,r) is xp+yq+zr=1
Given that this plane passes through (a,b,c).
∴ap+bq+cr=1
Equation of spere is x2+y2+z2−px−qy−rz=0
Centre of the sphere = (l, m, n)=(p2,q2,r2)
⇒p=2l,q=2m,r=2n
∴locus of the centre ⇒ax+by+cz=2
Topper's Solved these Questions
Similar Questions
A variable plane passes through a fixed point (a,b,c) and cuts the coordinate axes at points A,B,andC. Show that eh locus of the centre of the sphere OABCisax+by+cz=2.
View SolutionA variable plane passes through a fixed point (a,b,c) and meets the co-ordinate axes in A, B, C. Show that the locus of the point common to the planes through A, B, C parallel to the co-ordiante planes is ax+by+cz=1.
View Solution
Knowledge Check
A variable plane passes through a fixed point (a, b, c) and cuts the axes in A. B and C respectively. The locus of the centre of the sphere OABC. O being the origin.is
AA. xa+yb+zc=1BB. ax+by+cz=1CC. ax+by+cz=2DD. xa+yb+zc=2A variable line passes through a fixed point (a,b) and meets the coordinate axes in A and B. The locus of the point of intersection of lines through A, B parallel to coordinate axes is
Axa+yb=1Bax+by=1Cxa+yb=2Dxa+yb=3A variable plane passes through a fixed point (1,−2,3) and meets the coordinate axes at points A, B, C then the point of intersection of the planes through A, B, C parallel to the coordinate planes lies on:
Axy−(1/2)yz+(1/3)zx=6Byz−2zx+3xy=xyzCxy−2yz+3zx=3xyzDxy+(1/2)yz−(1/3)zx=6
A variable plane passes through a fixed point (a,b,c) and cuts the coordinate axes at points A,B,andC. Show that eh locus of the centre of the sphere OABCisax+by+cz=2.
View SolutionA variable straight line passes through a fixed point (a,b) intersecting the co-ordinates axes at A & B. If 'O' is the origin, then the locus of the centroid of the triangle OAB is (A) bx+ay−3xy=0 (B) bx+ay−2xy=0 (C) ax+by−3xy=0 (D) ax+by−2xy=0.
View SolutionA variable plane passes through a fixed point (α,β,γ) and meets the axes at A,B,andC. show that the locus of the point of intersection of the planes through A,BandC parallel to the coordinate planes is αx−1+βy−1+γz−1=1.
View SolutionA variable plane passes through a fixed point (1,−2,3) and meets the coordinate axes at point A, B, C then the point of intersection of the planes through A, B, C parallel to the coordinate planes lies on
View SolutionIf a variable plane which is at a constant distance 3p from the origin cut the co-ordinate axes at points A ,B , C , then locus of the centroid of ΔABC is
View Solution
