Coordinates of the point O, P, Q and R are respectively (0,0,4),(4,6,2m),(2,0,2n) and (2,4,6). Let L,M,N and K be points on the sides OR, OP, PQ and QR respectively such that LMNK is a parallelogram whose two adjecent sides LM and side LK are each of length √2. What are the values of m and n respectively ?
6,2
1,3
3,1
None of the above
The correct Answer is:C
To solve the problem, we need to find the values of m and n given the coordinates of points O,P,Q,R and the conditions for the parallelogram LMNK. Here are the steps to arrive at the solution:
Step 1: Identify the Coordinates
The coordinates of the points are given as:
- O(0,0,4)
- P(4,6,2m)
- Q(2,0,2n)
- R(2,4,6)
Step 2: Find the Midpoints
Let’s find the coordinates of points M and L using the midpoint formula. The midpoint M of segment OP is given by:
M=(x1+x22,y1+y22,z1+z22)
Substituting O and P:
M=(0+42,0+62,4+2m2)=(2,3,m+2)
The midpoint L of segment OR is:
L=(0+22,0+42,4+62)=(1,2,5)
Step 3: Calculate Lengths of Sides
We know that the lengths of adjacent sides LM and LK are each √2.
Length LM:
Using the distance formula:
LM=√(xM−xL)2+(yM−yL)2+(zM−zL)2
Substituting the coordinates of L and M:
LM=√(2−1)2+(3−2)2+((m+2)−5)2=√12+12+(m−3)2
Setting this equal to √2:
√2+(m−3)2=√2
Squaring both sides:
2+(m−3)2=2⟹(m−3)2=0⟹m=3
Step 4: Find Length LK
Now we need to find LK. The coordinates of K are on segment QR:
K=(2+22,0+42,2n+62)=(2,2,n+3)
Now calculate LK:
LK=√(2−1)2+(2−2)2+((n+3)−5)2=√12+02+(n−2)2
Setting this equal to √2:
√1+(n−2)2=√2
Squaring both sides:
1+(n−2)2=2⟹(n−2)2=1⟹n−2=±1
Thus, n=3 or n=1.
Final Values
The values of m and n are:
m=3,n=3 or n=1
The coordinates of the points are given as:
- O(0,0,4)
- P(4,6,2m)
- Q(2,0,2n)
- R(2,4,6)
Let’s find the coordinates of points M and L using the midpoint formula. The midpoint M of segment OP is given by:
M=(x1+x22,y1+y22,z1+z22)
Substituting O and P:
M=(0+42,0+62,4+2m2)=(2,3,m+2)
L=(0+22,0+42,4+62)=(1,2,5)
We know that the lengths of adjacent sides LM and LK are each √2.
Using the distance formula:
LM=√(xM−xL)2+(yM−yL)2+(zM−zL)2
Substituting the coordinates of L and M:
LM=√(2−1)2+(3−2)2+((m+2)−5)2=√12+12+(m−3)2
Setting this equal to √2:
√2+(m−3)2=√2
Squaring both sides:
2+(m−3)2=2⟹(m−3)2=0⟹m=3
Now we need to find LK. The coordinates of K are on segment QR:
K=(2+22,0+42,2n+62)=(2,2,n+3)
LK=√(2−1)2+(2−2)2+((n+3)−5)2=√12+02+(n−2)2
Setting this equal to √2:
√1+(n−2)2=√2
Squaring both sides:
1+(n−2)2=2⟹(n−2)2=1⟹n−2=±1
Thus, n=3 or n=1.
The values of m and n are:
m=3,n=3 or n=1
Topper's Solved these Questions
Similar Questions
Knowledge Check
OPQR is a square with M and N as the middle points of the sides PQ and QR, respectively. The ratio of the areas of the square and the triangle OMN is
A4:1B2:1C8:3D4:3In △PQR L and M are two points on the sides PQ and PR respectively such that LMII QR. If PL = 2cm, LQ = 6 cm and PM= 1.5 cm, then MR (in cm) is
A0.5B4.5C9D8OPQR is a square with M and N as the middle points of the sides PQ and QR, respectively. The ratio of the areas of the square and the triangle OMN is
A4:1B2:1C8:3D4:3
In ΔPQR, if PQ=QR and L,M and N are the mid-points of the sides PQ,QR and RP respectively. Prove that LN=MN.

View SolutionThe coordinates of the points A and B are, respectively, (-3, 2) and (2, 3). P and Q are points on the line joining A and B such that AP = PQ = QB. A square PQRS is constructed on PQ as one side, the coordinates of R can be
View SolutionIn Fig. 4.238, S and T are points on the sides PQ and PR respectively of PQR such that PT=2cm , TR=4cm and ST is parallel to QR . Find the ratio of the areas of PST and PQR . (FIGURE)
View Solution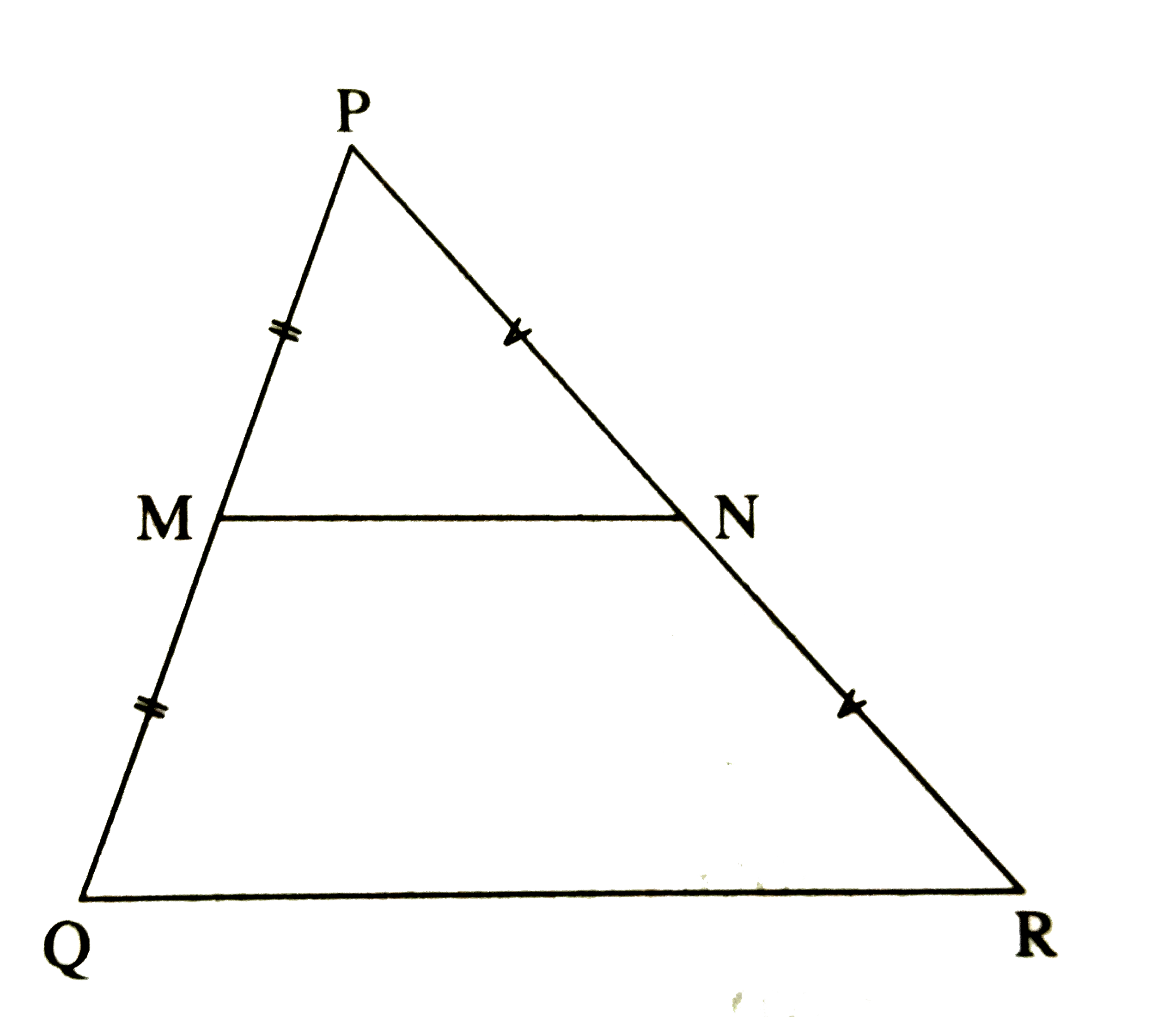
In the figure, M and N are the midpoints of sides PQ and PR respectively . If MN =6 cm then find QR. State your reason .
View SolutionIn PQR , M and N are points on sides PQ and PR respectively such that PM=15cm and NR=8cm . If PQ=25cm and PR=20cm state whether MNQR .
View Solution