Let f:R∈R be given by
f(x)={|x−[x]|when[x]is odd|x−[x]−1|when [x] is even where [*] denots the greatest integer function, then ∫4−2f(x)dx is equal to

A

52

B

32

C

5

D

3

Video Solution
Doubtnut Promotions Banner
Text Solution
Verified by Experts

The correct Answer is:D

We have,
f(x)={|x−[x]|when[x]is odd|x−[x]−1|when [x] is even [∴[x+1]=[x]+1]:}
⇒f(x)={{x}when[x]is odd1−{x}when [x] is even
The graph of f(x) is as shown in Fig. 12.
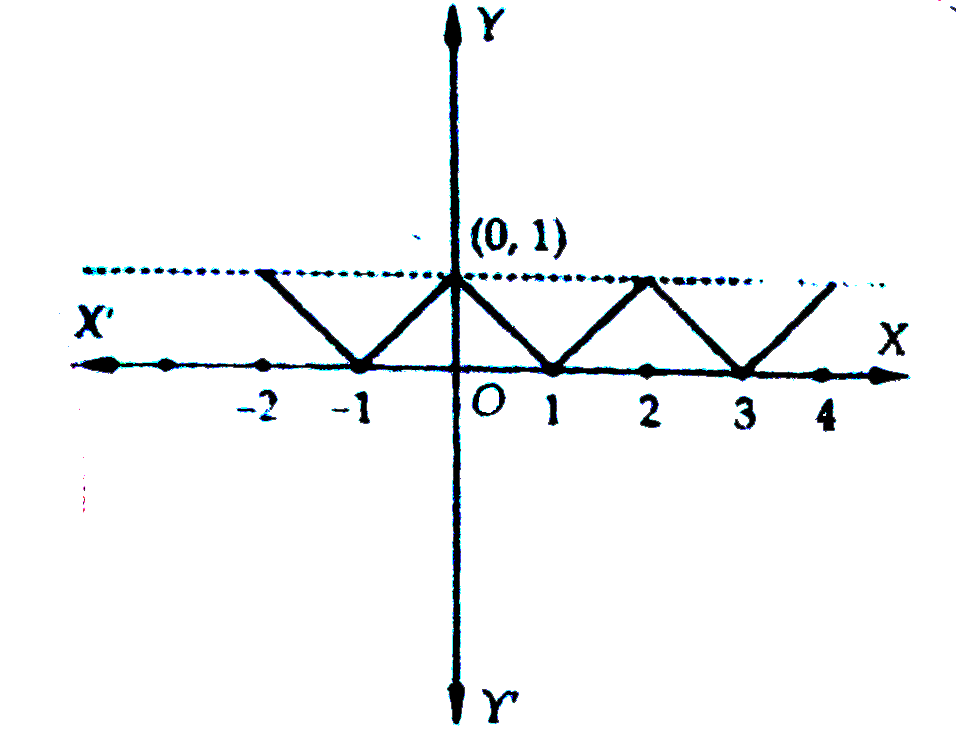
ocr_image
Clearly, 4∫−2f(x)dx=6−1∫−2f(x)dx=6×12=3

Updated on:21/07/2023
|
Class 12MATHSDEFINITE INTEGRAL

Topper's Solved these Questions

Similar Questions

Knowledge Check

  • If f(x)=[x]−[x4],x∈R where [x] denotes the greatest integer function, then

    Alimx→4+f(x) exists but limx→4−f(x) does not exist
    Bf is continuous at x=4
    CBoth limx→4−f(x)andlimx→4+f(x) exist but are not equal
    Dlimx→4−f(x) exists but limx→4+f(x) does not exist

  • Let f be an odd function then ∫1−1(|x|+f(x)cosx)dx is equal to

    A0
    B1
    C2
    Dnone of these

  • If f(x)=[x]|x|,x≠0, where [.] denotes the greatest integer function, then f'(1) is

    A−1
    B1
    Cnon-existent
    Dnone of these